Approximate Reciprocal Square Root

• Two Newton’s Methods
• Floating-Point as an Integer
• Finding a Magic Number
• Comparison with Known Magic Numbers
• Approximate Square Root
• Approximate Cube Root
• References

Two Newton’s Methods

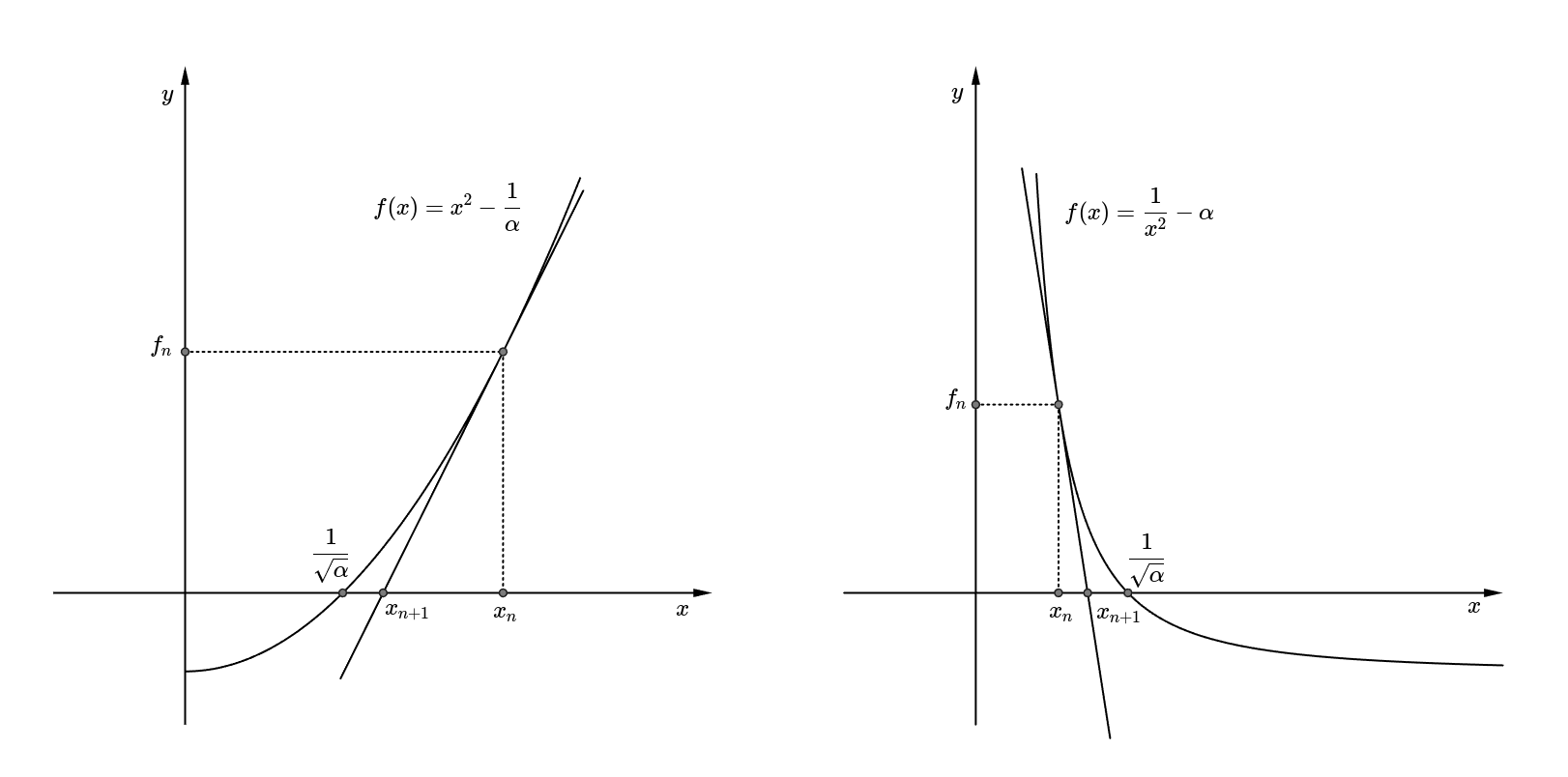
It seems natural to come up with Newton’s method to compute the reciprocal square root because it is a well-known technique for computing the square root. Although $f(x) = 1/x^2 - \alpha$ is the general approach, I thought $f(x) = x^2 - 1/\alpha$ could be another candidate for this problem. Applying Newton’s method to each case, the update formula can be obtained as follows. Note that $\alpha > 0$ in this note. $$\begin{aligned} x_n - \frac{f_n}{f'_n} \implies \begin{cases} \; x_{n + 1} = x_n - \cfrac{x_n^2 - 1/\alpha}{2 x_n} = \cfrac{x_n^2 + 1/\alpha}{2 x_n} = \cfrac{1}{2} \left( x_n + \cfrac{1}{\alpha x_n} \right) \\\\ \; x_{n + 1} = x_n - \cfrac{1/x_n^2 - \alpha}{-2 / x_n^3} = x_n + \cfrac{x_n - \alpha x_n^3}{2} = \cfrac{x_n (3 - \alpha x_n^2)}{2} \end{cases} \end{aligned}$$

While I could guess why $f(x) = x^2 - 1/\alpha$ is not used since it requires the division operation for every update, it is not sure which function is much harder to set the initial guess at first glance. For now, assume that $f(x) = 1/x^2 - \alpha$.

Floating-Point as an Integer

In the well-known fast approximate reciprocal square root algorithm, the surprising main idea, at least I think, is the integer representation of a floating-point. This itself is also a well-known trick, but it is quite surprising at the fact that this can be used to estimate the initial guess of Newton’s method. Since $\alpha > 0$, let $\alpha = 2^{E - 127}(1 + M)$ where $E$ is the exponent and $M$ is from the mantissa field such that $(1.d_1d_2\dots d_{23})_2 = 1 + M$ according to this note. Note that $E$ is an integer such that $1 \leq E \leq 254$, and $M$ is a real number such that $0 \leq M < 1$. To the further discussion, the integer representation $I_\alpha$ of $\alpha$ can be written as $$\begin{aligned} I_\alpha &= E \cdot 2^{23} + \left( d_1 \cdot 2^{22} + d_2 \cdot 2^{21} + \cdots + d_{23} \cdot 2^{0} \right) \\\\ &= E \cdot 2^{23} + 2^{23} \left( d_1 \cdot 2^{-1} + d_2 \cdot 2^{-2} + \cdots + d_{23} \cdot 2^{-23} \right) \\\\ &= E \cdot 2^{23} + M \cdot 2^{23} = (E + M) 2^{23} \end{aligned}$$

Now, to infer $I_{\alpha^{-1/2}}$, at first $\alpha^{-1/2}$ can be reformed to look similar to $\alpha$ as follows. $$\begin{aligned} \alpha^{-1/2} &= 2^{127/2 - E/2} (1 + M)^{-1/2} = 2^{(127/2 - E/2 + 127) - 127} (1 + M)^{-1/2} \\ &= 2^{(190.5 - E/2) - 127} (1 + M)^{-1/2} \end{aligned}$$

Here, since $2^{-1/2} < (1 + M)^{-1/2} \leq 1$, a little adjustment can be applied to fall within the range $[1, 2)$, and finally $I_{\alpha^{-1/2}}$ can be approximated. $$\begin{aligned} \alpha^{-1/2} &= 2^{(190.5 - E/2) - 127} (1 + M)^{-1/2} \\ &= 2^{(190 - E/2) - 127} (1 + M)^{-1/2} 2^{0.5} \\ &\approx 2^{(190 - E/2) - 127} (1 + (1 - M) / 2) \\\\ \implies I_{\alpha^{-1/2}} &\approx (190 - E/2) 2^{23} + ((1 - M) / 2) 2^{23} \\ &= \left( 190 \cdot 2^{23} + 0.5 \cdot 2^{23} \right) - \left( (E/2) 2^{23} + (M/2) 2^{23} \right) \end{aligned}$$

Note that $0 < (1 + M)^{-1/2} 2^{0.5} - 1 \leq 2^{0.5} - 1 \approx 0.4142$ since $0 \leq M < 1$. As such, if shifting $I_x$ right one position and subtracting it from $190 \cdot 2^{23} + 0.5 \cdot 2^{23}$, this result might give a good initial guess for Newton’s method. The code from this may look like as follows. Note that 0x5f400000 is equal to $190 \cdot 2^{23} + 0.5 \cdot 2^{23}$.

float rsqrt(float a)
{
    union { int xi; float x; };

    x = a;
    float a_half = 0.5f * a;
    xi = 0x5f400000 - (xi >> 1); // approximation to get the initial guess
    x = x * (1.5f - a_half * x * x); // one iteration of Newton's method
    return x;
}

However, this code seems not that accurate, so deep analysis is required to find a better value than 0x5f400000. Even though more iterations of Newton’s method may give a better result, it is much more efficient to get a better initial guess. More specifically, magic - (xi >> 1) should be well approximated to $I_{\alpha^{-1/2}}$ for a magic number magic.

Finding a Magic Number

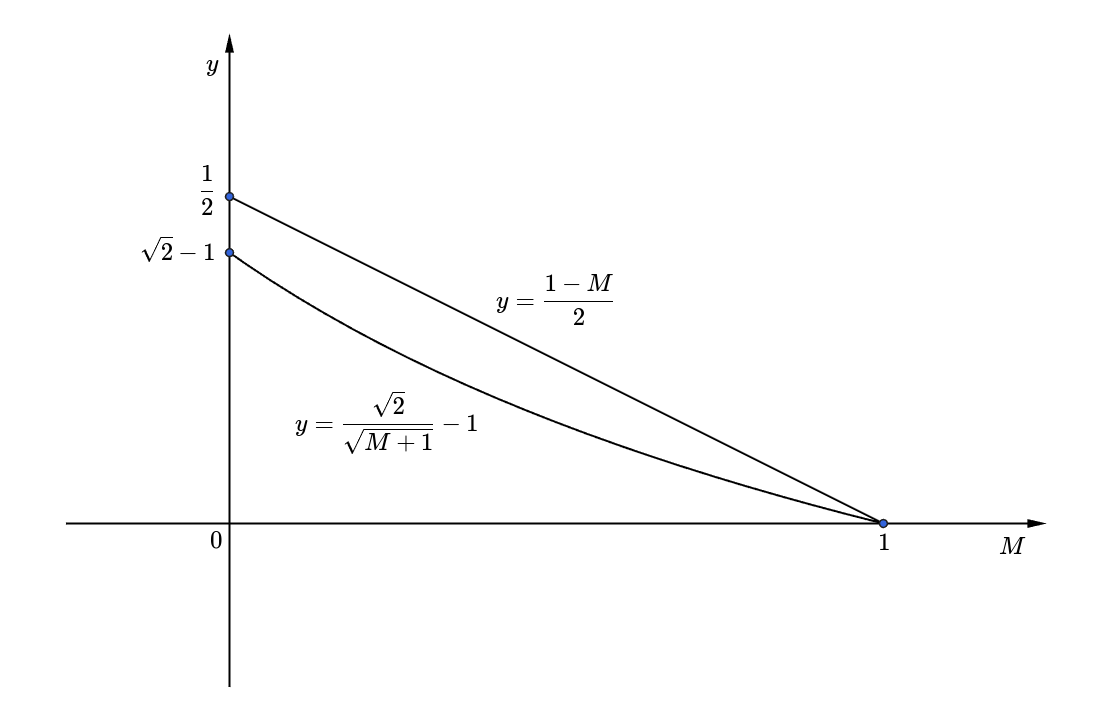
There are a few approaches to finding a magic number with an approximate logarithm or minimizing the relative error. But, I got an idea from the previous section while analyzing the mantissa field to set the rough initial guess, 0x5f400000. Let $m$ be this magic number and $m = 2^{E_m - 127}(1 + M_m)$. Then, the main goal is to find the optimal $m$ such that $$\begin{aligned} I_{\alpha^{-1/2}} &\approx I_m - \left( (E/2) 2^{23} + (M/2) 2^{23} \right) \\\\ &= \left( E_m \cdot 2^{23} + M_m \cdot 2^{23} \right) - \left( (E/2) 2^{23} + (M/2) 2^{23} \right) \end{aligned}$$

The important thing is that the form $M/2$ must be maintained while processing the optimization due to the (xi >> 1) part. In other words, since $\alpha^{-1/2}$ had been approximated with a line whose slope is $-M/2$ in the previous section, the (xi >> 1) part was able to be possible. As such, this slope must be maintained and the line can move only up and down by a real number $t$. This situation is as below. $$\begin{aligned} \alpha^{-1/2} &= 2^{(190 - E/2) - 127} (1 + M)^{-1/2} 2^{0.5} \\ &\approx 2^{(190 - E/2) - 127} (1 + (t - M) / 2) \end{aligned}$$

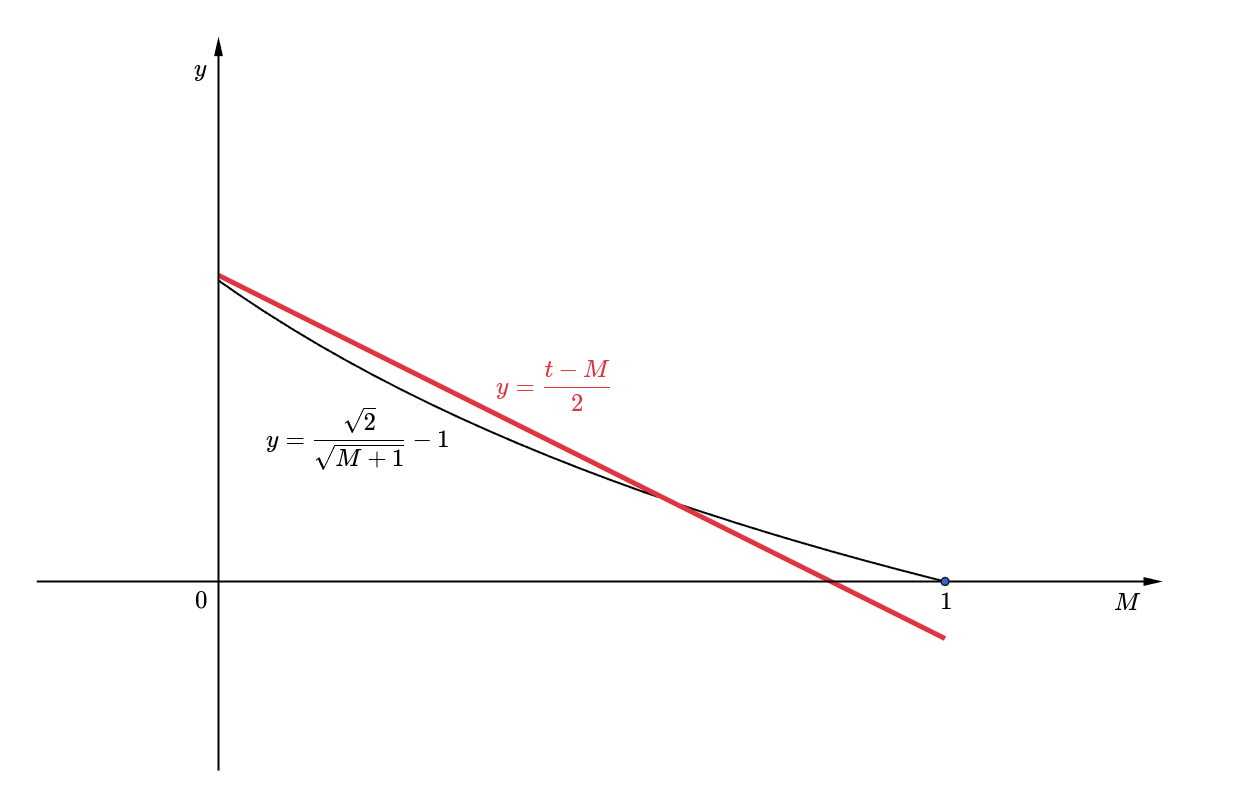
Therefore, optimizing this line for $\alpha^{-1/2}$ is equal to finding the optimal $t^*$ minimizing the following cost function $g(t)$ using Least squares. $$\begin{aligned} \argmin_{t} g(t) = \argmin_{t} \int_{0}^{1} \left( \cfrac{t - M}{2} - \left( \cfrac{\sqrt{2}}{\sqrt{M+1}} - 1 \right) \right)^2 dM \end{aligned}$$

Unfolding $g(t)$, $$\begin{aligned} g(t) &= \int_{0}^{1} \cfrac{t^2 - 2tM + M^2}{4} - (t-M) \left( \cfrac{\sqrt{2}}{\sqrt{M+1}} - 1 \right) + \left( \cfrac{\sqrt{2}}{\sqrt{M+1}} - 1 \right)^2 dM \\\\ &= \int_{0}^{1} \cfrac{t^2}{4} - \cfrac{tM}{2} + t\left( 1 - \cfrac{\sqrt{2}}{\sqrt{M+1}} \right) + h(M) dM \\\\ &= \left[ \cfrac{t^2}{4}M - \cfrac{t}{4}M^2 + tM - 2t \sqrt{2} \sqrt{M+1} \right]_{0}^{1} + \int_{0}^{1} h(M) dM \\\\ &= \cfrac{t^2}{4} - \cfrac{t}{4} + t - 2\sqrt{2}(\sqrt{2} - 1)t + \int_{0}^{1} h(M) dM \\\\ &\implies g'(t) = \cfrac{t}{2} - \cfrac{1}{4} + 1 - 4 + 2\sqrt{2} = \cfrac{t}{2} - \cfrac{13}{4} + 2\sqrt{2} = 0 \\\\ &\implies t^* = \cfrac{13 - 8\sqrt{2}}{2} \end{aligned}$$

Note that $h(M)$ does not even have to be considered because it will be canceled out and $t^*$ is the right one minimizing $g(t)$ since it is a convex function. $$\begin{aligned} I_{\alpha^{-1/2}} &\approx (190 - E/2) 2^{23} + ((t^* - M) / 2) 2^{23} \\ &= \left( 190 \cdot 2^{23} + t^*/2 \cdot 2^{23} \right) - \left( (E/2) 2^{23} + (M/2) 2^{23} \right) \end{aligned}$$

Accordingly, the found optimal magic number is $I_m = 190 \cdot 2^{23} + (3 - 8\sqrt{2}) \cdot 2^{21} \approx 1597371930$, which is equal to 0x5f35f61a.

Comparison with Known Magic Numbers

There are already known magic numbers such as 0x5f375a86 and 0x5f37599e. Compared with these magic numbers, it is found that 0x5f35f61a does not perform that better than them after Newton’s steps. It is not that surprising, however, because as Lomont points out, his first optimal constant 0x5f37642f based on the analysis rather showed slightly less accuracy than 0x5f375a86 he found from the trial-and-error. 0x5f37599e is the known best magic number from [1] although no detailed explanation. Although 0x5f35f61a has the higher maximum relative error for all floating-point values, it has not been always the case and was not even rare while testing. So, it might be useful in some situations.

float rsqrt(float a)
{
    union { int xi; float x; };

    x = a;
    float a_half = 0.5f * a;
    //xi = 0x5f35f61a - (xi >> 1);
    xi = 0x5f37599e - (xi >> 1);
    x = x * (1.5f - a_half * x * x);
    return x;
}

In modern C++, std::bit_cast is supported through C++20’s, and it can replace union statement.

# include <bit>
# include <limits>
# include <cstdint>

constexpr float rsqrt(float a) noexcept
{
    static_assert( std::numeric_limits<float>::is_iec559 ); // (enable only on IEEE 754)

    //const float x = std::bit_cast<float>(0x5f35f61a - (std::bit_cast<std::uint32_t>(a) >> 1));
    const float x = std::bit_cast<float>(0x5f37599e - (std::bit_cast<std::uint32_t>(a) >> 1));
    return x * (1.5f - a * 0.5f * x * x);
}

Furthermore, when applying Newton’s method for $f(x) = x^2 - 1/\alpha$, it seems that the relative error is much smaller. However, as mentioned before, it requires division operation, so it might be the reason that it is not used since it is not suited for fast approximation. Besides, it is worth noting, according to Wikipedia, this algorithm is not generally the best choice for modern computers with subsequent hardware advancements, especially the x86 SSE instruction rsqrtss.

Approximate Square Root

Similarly, the approximate square root function can be derived. $$\begin{aligned} \alpha^{1/2} &= 2^{(63.5 + E/2) - 127} (1 + M)^{1/2} \\\\ \implies I_{\alpha^{1/2}} &\approx (63 + E/2) 2^{23} + (t + M / 2) 2^{23} \\ \end{aligned}$$

The known optimal magic number is 0x1fbb67a8, the code is as below. The used $f(x)$ for Newton’s method is the same as the one in this note.

float sqrt(float a)
{
    union { int xi; float x; };

    x = a;
    xi = 0x1fbb67a8 + (xi >> 1);
    x = 0.5f * (x + a / x);
    return x;
}

Approximate Cube Root

Interestingly, the approximate cube root function can be derived as well. The main problem is now $E/3$ and $M/3$ since it is not the square root using only $E/2$ and $M/2$, which work fine with the right shift operation. However, the division by 3 can be approximately implemented with the right shifts as well. $$\begin{aligned} \cfrac{x}{3} \approx \cfrac{x}{2^2} + \cfrac{x}{2^4} + \cfrac{x}{2^6} + \cdots + \cfrac{x}{2^{16}} \end{aligned}$$

This can be evaluated with 7 instructions and slight improvement is also known as below.

float cbrt(float a)
{
    union { int xi; float x; };

    x = a;
    xi = (xi >> 2) + (xi >> 4); // approximate divide by 3
    xi += xi >> 4;
    xi += xi >> 8;
    xi += 0x2a5137a0;
    x = 0.33333333f * (2.0f * x + a / (x * x));
    return x;
}

But, this method is not as successful as in the case of reciprocal square root and square root.

References

[1] Henry S. Warren. 2012. Hacker’s Delight (2nd. ed.). Addison-Wesley Professional.

[2] Fast inverse square root

[3] FAST INVERSE SQUARE ROOT - CHRIS LOMONT