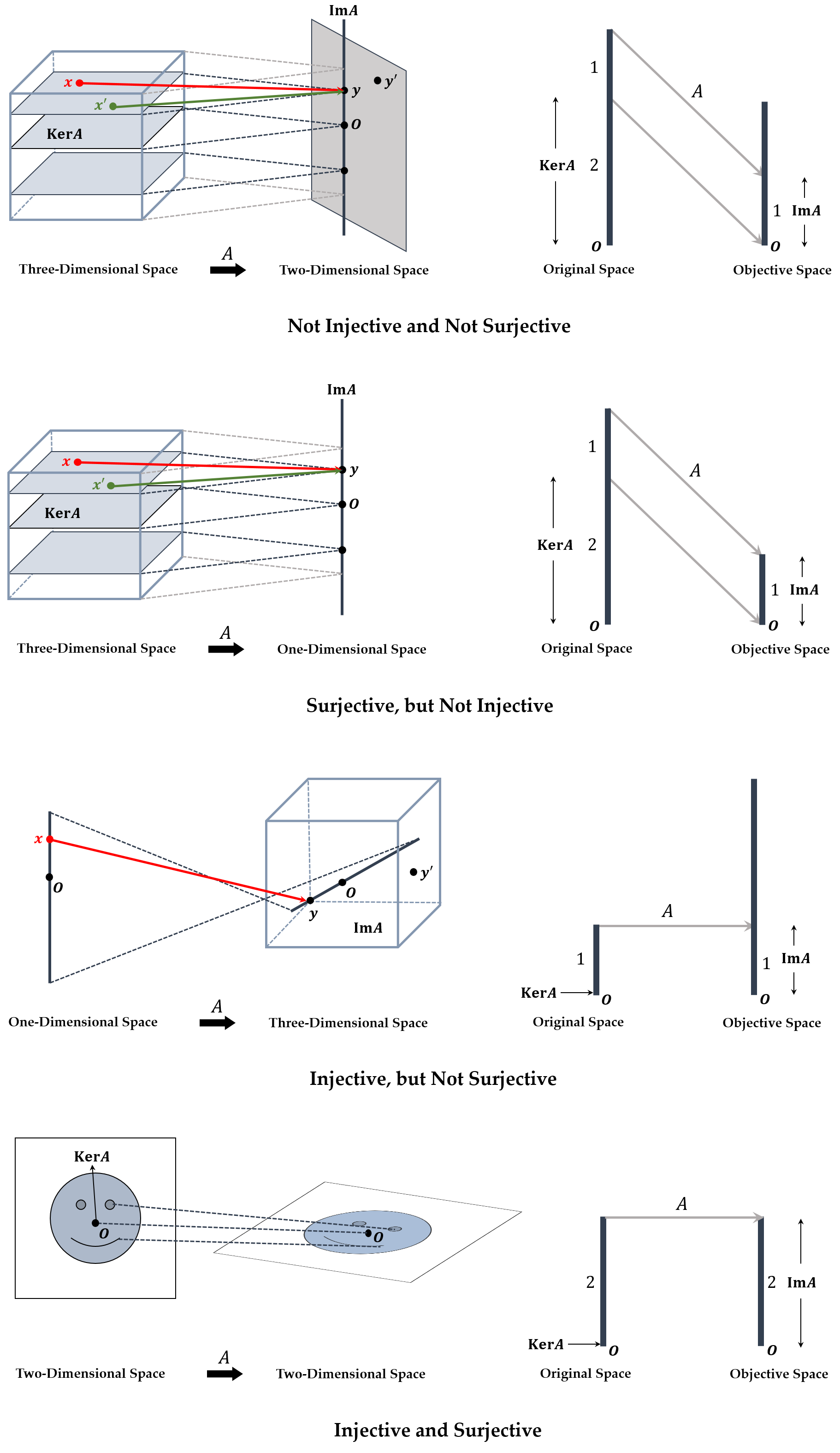
Rank Theorem

• For an $m \times n$ matrix $A$, it maps a point in $n$-dimension to one in $m$-dimension.

$$\begin{aligned} \dim \ker A + \dim Im A = \dim \ker A + rank A = n \end{aligned}$$

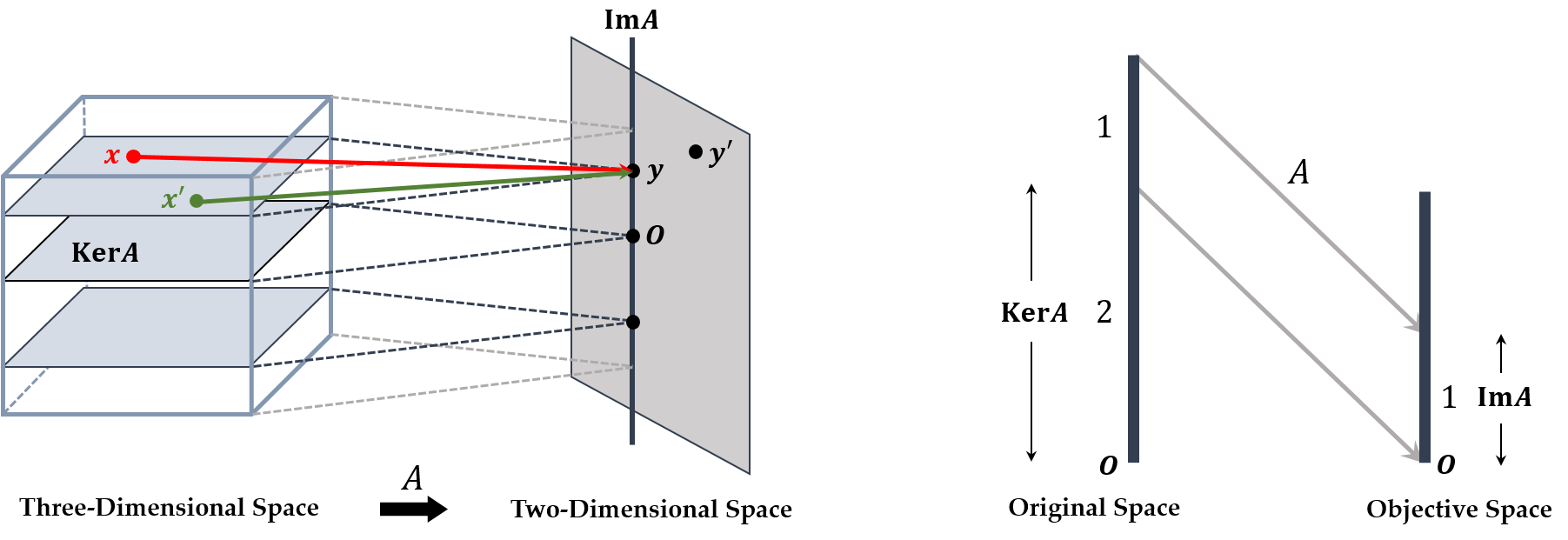
Original $n$-dimension is suppressed by $\dim \ker A$ and mapped by $\dim Im A = rank A$ to the objective space.

• If $m > n$, the mapping by $A$ is to the higher dimension. However, it cannot cover that dimension all.
• If $m < n$, the mapping by $A$ is to the lower dimension. So, many points map to one point, which means a kind of suppression.
• Let $Ax = y$. For $x_1$ and $x_2$, if $x_1 = x_2$ when $y = Ax_1 = Ax_2$, then $A$ is injective. If there exists $x$ such that $y = Ax$ for all $y$, then $A$ is surjective.
• $rank A \le m$. It means that the objective space is $m$-dimensional, so $\dim Im A$ is at most $m$.
• $rank A \le n$. It means that the original space is $n$-dimensional, so $\dim Im A$ is at most $n$ although it covers the objective space all.

Reference

[1] Hiraoka Kazuyuki, Hori Gen, Programming No Tame No Senkei Daisu, Ohmsha.