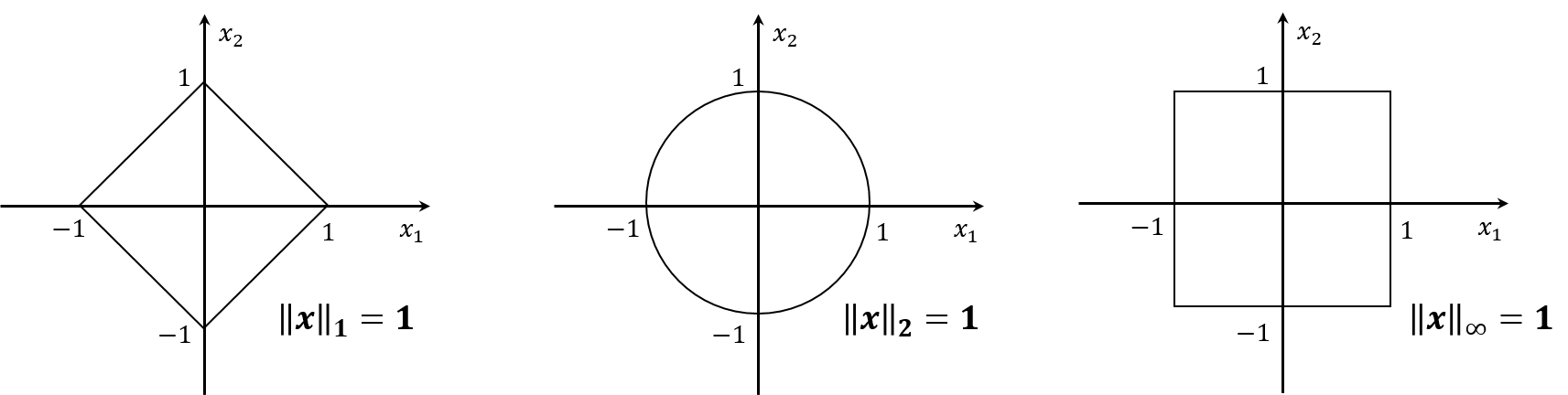
1. Vector Norms Let x = ( x 1 , ⋯ , x n ) t x = (x_1, \cdots, x_n)^t x = ( x 1 , ⋯ , x n ) t n × 1 n \times 1 n × 1
p p p ∥ x ∥ p = ( ∑ i = 1 n ∣ x i ∣ p ) 1 p \left\| x \right\|_p = \left(\sum_{i=1}^n \vert x_i \vert^p\right)^{\frac{1}{p}} ∥ x ∥ p = ( ∑ i = 1 n ∣ x i ∣ p ) p 1 1 1 1 ∥ x ∥ 1 = ∑ i = 1 n ∣ x i ∣ \left\| x \right\|_1 = \sum_{i=1}^n \vert x_i \vert ∥ x ∥ 1 = ∑ i = 1 n ∣ x i ∣ 2 2 2 Euclidean norm ): ∥ x ∥ 2 = ( ∑ i = 1 n ∣ x i ∣ 2 ) 1 2 \left\| x \right\|_2 = \left(\sum_{i=1}^n \vert x_i \vert^2\right)^{\frac{1}{2}} ∥ x ∥ 2 = ( ∑ i = 1 n ∣ x i ∣ 2 ) 2 1 ∞ \infty ∞ ∥ x ∥ ∞ = max ∣ x i ∣ \left\| x \right\|_{\infty} = \max \vert x_i \vert ∥ x ∥ ∞ = max ∣ x i ∣ ∥ x ∥ ∞ = lim p → ∞ ( ∑ i = 1 n ∣ x i ∣ p ) 1 p = lim p → ∞ ( ∣ x j ∣ p ) 1 p where j = arg max ∣ x i ∣ = max ∣ x i ∣ \begin{aligned} \left\| x \right\|_{\infty} &= \lim_{p \to \infty} \left(\sum_{i=1}^n \vert x_i \vert^p\right)^{\frac{1}{p}} = \lim_{p \to \infty} \left(\vert x_j \vert^p\right)^{\frac{1}{p}} \text{ where } j = \argmax \vert x_i \vert \\ &= \max \vert x_i \vert \end{aligned} ∥ x ∥ ∞ = p → ∞ lim ( i = 1 ∑ n ∣ x i ∣ p ) p 1 = p → ∞ lim ( ∣ x j ∣ p ) p 1 where j = arg max ∣ x i ∣ = max ∣ x i ∣ The graphs of ∥ x ∥ 1 = ∥ x ∥ 2 = ∥ x ∥ ∞ = 1 \left\| x \right\|_1 = \left\| x \right\|_2 = \left\| x \right\|_{\infty} = 1 ∥ x ∥ 1 = ∥ x ∥ 2 = ∥ x ∥ ∞ = 1 x ∈ R 2 x \in \R^2 x ∈ R 2
For any vector x ‾ \overline{x} x ∥ x ∥ ∞ ≤ ∥ x ∥ 2 ≤ ∥ x ∥ 1 \left\| x \right\|_{\infty} \le \left\| x \right\|_2 \le \left\| x \right\|_1 ∥ x ∥ ∞ ≤ ∥ x ∥ 2 ≤ ∥ x ∥ 1 x ‾ ∈ R 2 \overline{x} \in \R^2 x ∈ R 2
Meanwhile, ∥ x ∥ 1 ≤ n ∥ x ∥ 2 \left\| x \right\|_1 \le \sqrt{n} \left\| x \right\|_2 ∥ x ∥ 1 ≤ n ∥ x ∥ 2 ∥ x ∥ 2 ≤ n ∥ x ∥ ∞ \left\| x \right\|_2 \le \sqrt{n} \left\| x \right\|_{\infty} ∥ x ∥ 2 ≤ n ∥ x ∥ ∞ ∥ x ∥ 1 ≤ n ∥ x ∥ ∞ \left\| x \right\|_1 \le n \left\| x \right\|_{\infty} ∥ x ∥ 1 ≤ n ∥ x ∥ ∞ If ∥ x ∥ p > 0 \left\| x \right\|_p > 0 ∥ x ∥ p > 0 x ≠ 0 x \not = 0 x = 0 ∥ γ x ∥ p = ∣ γ ∣ ∥ x ∥ p \left\| \gamma x \right\|_p = \vert \gamma \vert \left\| x \right\|_p ∥ γ x ∥ p = ∣ γ ∣ ∥ x ∥ p γ ∈ R \gamma \in \mathbb{R} γ ∈ R ∥ x + y ∥ p ≤ ∥ x ∥ p + ∥ y ∥ p \left\| x + y \right\|_p \le \left\| x \right\|_p + \left\| y \right\|_p ∥ x + y ∥ p ≤ ∥ x ∥ p + ∥ y ∥ p ∣ ∥ x ∥ p − ∥ y ∥ p ∣ ≤ ∥ x − y ∥ p \vert \left\| x \right\|_p - \left\| y \right\|_p \vert \le \left\| x - y \right\|_p ∣ ∥ x ∥ p − ∥ y ∥ p ∣ ≤ ∥ x − y ∥ p 2. Matrix Norms Suppose that A A A m × n m \times n m × n a i j a_{ij} a ij ( i , j ) (i, j) ( i , j ) A A A ∥ A ∥ \left\| A \right\| ∥ A ∥ A A A x x x ∥ A ∥ = max x ≠ 0 ∥ A x ∥ ∥ x ∥ \begin{aligned} \left\| A \right\| = \max_{x \not = 0} \frac{\left\| Ax \right\|}{\left\| x \right\|} \end{aligned} ∥ A ∥ = x = 0 max ∥ x ∥ ∥ A x ∥
∥ A ∥ 1 = max ∑ i = 1 m ∣ a i j ∣ \left\| A \right\|_1 = \max \sum_{i=1}^m \vert a_{ij} \vert ∥ A ∥ 1 = max ∑ i = 1 m ∣ a ij ∣ largest column sum of A A A ∥ A ∥ 2 \left\| A \right\|_2 ∥ A ∥ 2 largest singular value of A A A A t A A^tA A t A When A A A A t A v = A ( λ v ) = λ 2 v A^tAv = A(\lambda v) = \lambda^2 v A t A v = A ( λ v ) = λ 2 v x x x λ \lambda λ A A A ∥ A ∥ 2 = λ max ( A t A ) = λ max ( A ) 2 = ∣ λ max ( A ) ∣ \begin{aligned} \left\| A \right\|_2 = \sqrt{\lambda_{\max} (A^t A)} = \sqrt{\lambda_{\max} (A)^2} = \vert \lambda_{\max} (A) \vert \end{aligned} ∥ A ∥ 2 = λ m a x ( A t A ) = λ m a x ( A ) 2 = ∣ λ m a x ( A ) ∣ ∥ A ∥ ∞ = max ∑ i = 1 n ∣ a i j ∣ \left\| A \right\|_{\infty} = \max \sum_{i=1}^n \vert a_{ij} \vert ∥ A ∥ ∞ = max ∑ i = 1 n ∣ a ij ∣ largest row sum of A A A ∥ A ∥ > 0 \left\| A \right\| > 0 ∥ A ∥ > 0 A ≠ O A \not = O A = O ∥ γ A ∥ = ∣ γ ∣ ∥ A ∥ \left\| \gamma A \right\| = \vert \gamma \vert \left\| A \right\| ∥ γ A ∥ = ∣ γ ∣ ∥ A ∥ γ ∈ R \gamma \in \mathbb{R} γ ∈ R ∥ A + B ∥ ≤ ∥ A ∥ + ∥ B ∥ \left\| A + B \right\| \le \left\| A \right\| + \left\| B \right\| ∥ A + B ∥ ≤ ∥ A ∥ + ∥ B ∥ ∥ A B ∥ ≤ ∥ A ∥ ∥ B ∥ \left\| AB \right\| \le \left\| A \right\| \left\| B \right\| ∥ A B ∥ ≤ ∥ A ∥ ∥ B ∥ ∥ A x ∥ ≤ ∥ A ∥ ∥ x ∥ \left\| Ax \right\| \le \left\| A \right\| \left\| x \right\| ∥ A x ∥ ≤ ∥ A ∥ ∥ x ∥ Reference [1] Michael T. Heath, Scientific Computing: An Introductory Survey. 2nd Edition, McGraw-Hill Higher Education.
© 2026. All rights reserved.