Properties of Projection Matrix

1. Projection matrix has a null vector.

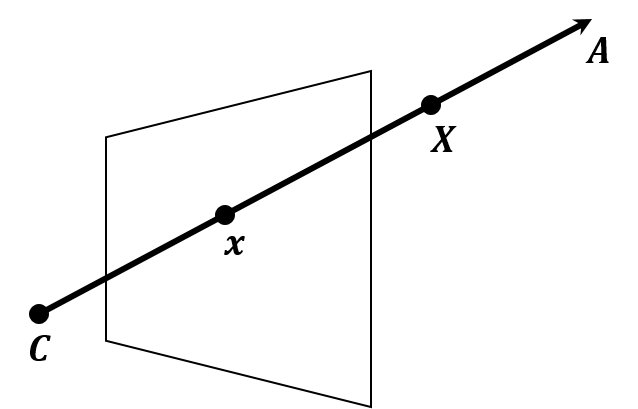
NullVector

Projection matrix $P$ is a $3 × 4$ matrix, so it must have a null vector. This null vector is the center $C$ of the camera.
For some point $A$ , there exists a point $X$ on the line passing through points $A$ and $C$ . In other words, therer is a $\lambda \in \R$ such that $X = C + \lambda A$ . Let $x$ be the image of $X$ , then $x = PX = P(C + \lambda A) = PC + \lambda PA = \lambda PA$ .
All the points on the line passing through points $A$ and $C$ are projected on the same image $x$ .
If $A$ moves, then the image $x$ is moved as well.
$C$ satisfied with this property is the only one, the center of the camera.

Let $P = [p_1 \vert p_2 \vert p_3 \vert p_4]$ where $p_i$ is a column vector.
In world coordinates, the points which are located on $x$ , $y$ , and $z$ -axis at infinity are $(1, 0, 0, 0)^t$ , $(0, 1, 0, 0)^t$ , and $(0, 0, 1, 0)^t$ .
The images of these points are $P(1, 0, 0, 0)^t = p_1$ , $P(0, 1, 0, 0)^t = p_2$ , and $P(0, 0, 1, 0)^t = p_3$ .
The image of the origin in world coordinates is $P(0, 0, 0, 1)^t = p_4$ ,
To sum up, $p_1$ , $p_2$ , and $p_3$ are the images of points on $x$ , $y$ , and $z$ -axis at infinity. $p_4$ is the image of the origin in world coordinates.

RowVector

Let $P = [p^{1t} \vert p^{2t} \vert p^{3t}]^t$ where $p^i$ is a row vector.
For the point $X$ on the principle plane which is parallel with the image plane and passes through the camera center, $PX = (x, y, 0)^t$ form.
Since the line passing through points $C$ and $X$ is parallel with the image plane, this line intersects with the image plane at infinity whose image is also at infinity.
$p^{3t}X = 0$ , which means that $X$ is on the plane $p^3$ .
In the same way, the point $Y$ such that $PY = (0, y, w)^t$ is on the plane $p^1$ and the point $Z$ such that $PZ = (x, 0, w)^t$ is on the plane $p^2$ .

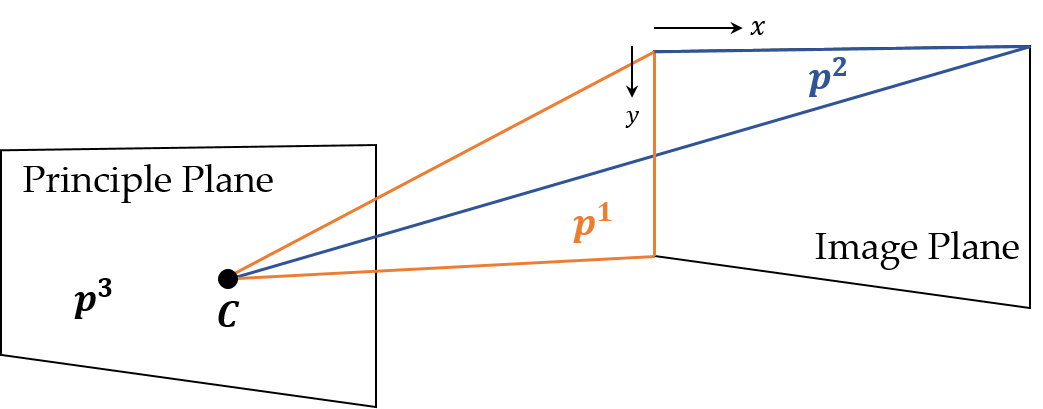
RowPlane

$p^1$ and $p^2$ are called axis planes, and $p^3$ is called the principle plane.

Principle axis is the line passing through point $C$ and perpendicular to the principle plane. So $p^3$ is the normal vector of the principle plane.
The point $q$ in the normal direction of the principle plane at infinity is $q = (p^{3t}_{11}, p^{3t}_{21}, p^{3t}_{31}, 0)^t$ where $p^{3t}_{ij}$ is the $(i, j)$ element of $p^3$ .
The image of $q$ is called principle point.

For an image $x$ , its world point is $P^{+}x$ where $P^{+} = P^t (PP^t)^{-1}$ .
$P(P^{+}x) = P(P^t (PP^t)^{-1}x) = PP^t (PP^t)^{-1}x = x$ .
As $rank(P) = 3$ , $PP^{+}$ is full-rank. So, $PP^{+}$ is invertible.
For the ray passing through point $C$ and the image $x$ , an arbitrary point $X$ on this ray can be represented as a linear combination such that $X = C + \lambda P^{+}x$ .

[1] Hartley, R. and Zisserman, A. (2003) Multiple View Geometry in Computer Vision. 2nd Edition, Cambridge University Press, Cambridge.