Faster Bresenham's Algorithm

• Bresenham’s Algorithm Revisit
• Double Speed Bresenham’s Algorithm
• Symmetry
• References

Bresenham’s Algorithm Revisit

The Bresenham’s algorithm is the most representative method to rasterize line segments, which uses only integer addition and subtraction. For convenience, assume that each point is the center of the pixel, not the lower left corner of the pixel. In other words, each element of the two endpoints $p_0 = (x_0, y_0)$ and $p_1 = (x_1, y_1)$ of a line segment is an integer, and the line segment connects the centers of these two pixels. Also, only consider lines where $x_0 < x_1$ and $y_0 < y_1$ and the slope is between $0$ and $1$. This is because it can be easily applied to other cases.

The line defined by two points $p_0$ and $p_1$ can be expressed as follows. Let $dx = x_1 - x_0$ and $dy = y_1 - y_0$. $$\begin{aligned} y = \frac{dy}{dx} x + b \end{aligned}$$

Here, when the slope value, which is a rational number, is multiplied by $dx$ on both sides to change it to an integer and then rearranged, it is expressed as the following implicit function. $$\begin{aligned} f(x, y) = x dy - y dx + b dx = 0 \end{aligned}$$

The advantage of an implicit function is that when a point $(x, y)$ is substituted into $f(x, y)$, if the value is 0, it means that the point is on the line. Also, if the value is positive, it means that it is below the line, and if it is negative, it means that it is above the line.

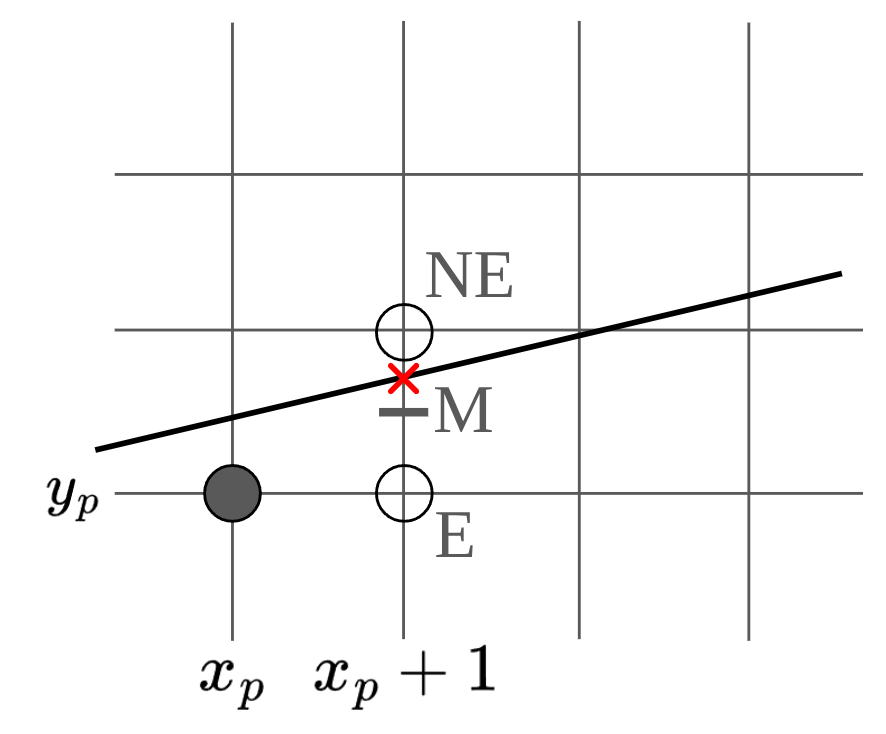
As shown in the figure above, say that $(x_p, y_p)$ is currently selected. Since only lines with slopes between 0 and 1 are considered, the next pixel to be selected is either E or NE. In order to decide which pixel to select, it would be reasonable to consider whether the line passes above or below the point M, which is the midpoint between N and NE. The figure above shows a situation in which NE must be selected.

More Specifically, the point M $(x_p + 1, y_p + 1/2)$ can be put into $f(x,y)$ as follows. $$\begin{aligned} f(x_p + 1, y_p + \frac{1}{2}) = (x_p + 1) dy - \left(y_p + \frac{1}{2} \right) dx + b dx = D \end{aligned}$$

Here, $D$ is called a decision variable. If its value is positive, pixel NE must be selected, and if it is negative, pixel E must be selected. If it is 0, either pixel can be selected. However, computing $D$ for the next selection at each iteration is unnecessary. This approach is the core of the Bresenham’s algorithm, which is to derive the relationship with the next decision variable.

First, consider the case where E is currently selected. That is, $(x_p + 1, y_p)$ is selected, so the next decision variable $D_{\text{next}}$ must be calculated for the point $(x_p + 2, y_p + 1/2)$. $$\begin{aligned} D_{\text{next}} &= f(x_p + 2, y_p + \frac{1}{2}) = (x_p + 2) dy - \left(y_p + \frac{1}{2} \right) dx + b dx \\ &= D + dy \end{aligned}$$

Second, if NE is selected, $D_{\text{next}}$ can be calculated in a similar way as follows. $$\begin{aligned} D_{\text{next}} &= f(x_p + 2, y_p + \frac{3}{2}) = (x_p + 2) dy - \left(y_p + \frac{3}{2} \right) dx + b dx \\ &= D + dy - dx \end{aligned}$$

Therefore, if $c_E = dy$ and $c_{NE} = dy - dx$ are defined in advance, $D_{\text{next}}$ can be obtained from one of them by simply performing integer addition.

The initial decision variable $D_0$ is also needed, which can be computed explicitly via the point $p_0$, but this computation requires an integer division operation. $$\begin{aligned} D_0 &= f(x_0 + 1, y_0 + \frac{1}{2}) = (x_0 + 1) dy - \left(y_0 + \frac{1}{2} \right) dx + b dx \\ &= x_0 dy - y_0 dx + b dx + dy - \frac{dx}{2} \\ &= f(x_0, y_0) + dy - \frac{dx}{2} \\ &= dy - \frac{dx}{2} \end{aligned}$$

Note that $f(x_0, y_0) = 0$ because the point $p_0$ is on the line. A very simple workaround to avoid the division operation is to multiply both sides of $f(x, y) = 0$ by $2$. As a result, the decision variables are updated as follows: $$\begin{aligned} D_0 = 2dy - dx, \quad c_E = 2dy, \quad c_{NE} = 2(dy - dx) \end{aligned}$$

void drawLine(int x0, int y0, int x1, int y1)
{
    int y = y0;
    const int dx = x1 - x0;
    const int dy = y1 - y0;
    const int c_e = dy + dy;
    int d = c_e - dx;
    const int c_ne = d - dx;
    for (int x = x0; x < x1; ++x) {
        setPixel( x, y );
        if (d <= 0) d += c_e;
        else {
            y++;
            d += c_ne;
        }
    }
}

Double Speed Bresenham’s Algorithm

While Bresenham’s algorithm selects one next pixel, this can be improved in order to select the next two pixels. While Bresenham’s algorithm selects one next pixel, this can be improved in order to select the next two pixels. To obtain this efficiency, more cases should be considered than the original. That is, this time, only consider lines where the slope is between $0$ and $1/2$. And the rest cases can be easily applied from this case.

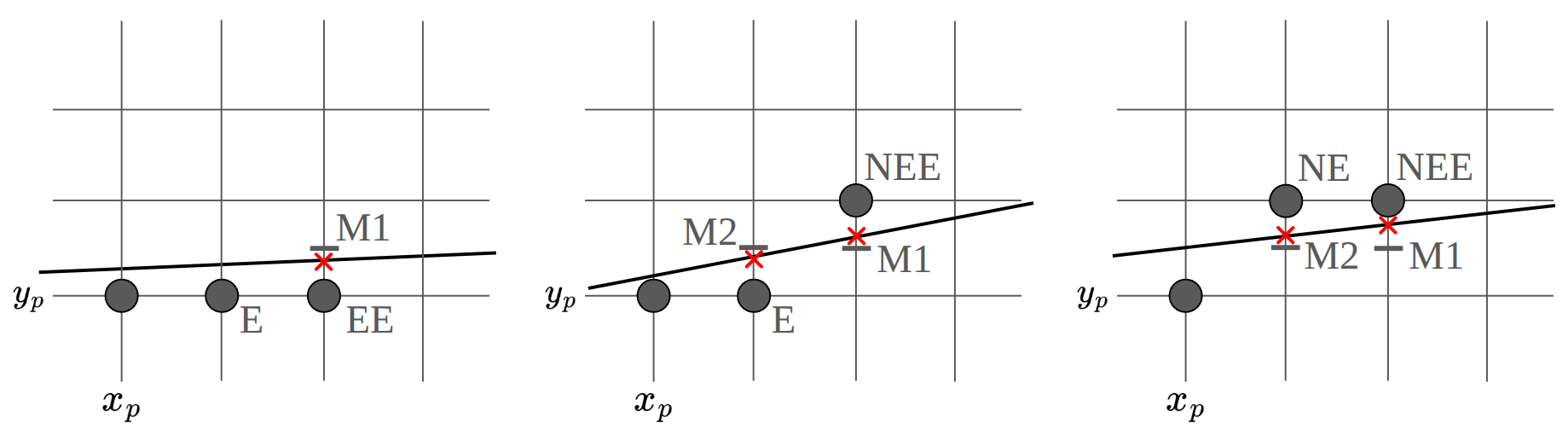
As previous, $(x_p, y_p)$ is currently selected pixel. Since the slope is between $0$ and $1/2$, the decisions that can be made are all 3 as above. As such, the two decision variables are needed due to considering the next two pixels. More specifically, the point M1 $(x_p + 2, y_p + 1/2)$ and the point M2 $(x_p + 1, y_p + 1/2)$ should be put into $f(x,y)$. $$\begin{aligned} f(x_p + 2, y_p + \frac{1}{2}) &= (x_p + 2) dy - \left(y_p + \frac{1}{2} \right) dx + b dx = D \\ f(x_p + 1, y_p + \frac{1}{2}) &= (x_p + 1) dy - \left(y_p + \frac{1}{2} \right) dx + b dx = D - dy \end{aligned}$$

Note that the practically required decision variable is only one, $D$, to make two decisions. With this, in order to derive the relationship with the next decision variable, the following cases should be considered.

First, consider the case where EE is currently selected. That is, $(x_p + 2, y_p)$ is selected, so the next decision variable $D_{\text{next}}$ is from the point $(x_p + 4, y_p + 1/2)$. $$\begin{aligned} D_{\text{next}} &= f(x_p + 4, y_p + \frac{1}{2}) = (x_p + 4) dy - \left(y_p + \frac{1}{2} \right) dx + b dx \\ &= D + 2 dy \end{aligned}$$

Second, if NEE is selected, $D_{\text{next}}$ can be calculated in a similar way as follows. $$\begin{aligned} D_{\text{next}} &= f(x_p + 4, y_p + \frac{3}{2}) = (x_p + 4) dy - \left(y_p + \frac{3}{2} \right) dx + b dx \\ &= D + 2 dy - dx \end{aligned}$$

So, the predefined $c_{EE} = 2 dy$ and $c_{NEE} = 2 dy - dx$ can be used this time. Besides, the initial decision variable $D_0$ can also be obtained via the point $p_0$. $$\begin{aligned} D_0 &= f(x_0 + 2, y_0 + \frac{1}{2}) = (x_0 + 2) dy - \left(y_0 + \frac{1}{2} \right) dx + b dx \\ &= x_0 dy - y_0 dx + b dx + 2 dy - \frac{dx}{2} \\ &= f(x_0, y_0) + 2 dy - \frac{dx}{2} \\ &= 2 dy - \frac{dx}{2} \end{aligned}$$

If multiplying both sides of $f(x, y) = 0$ by $2$ to avoid the division operation, the decision variables are finally updated as follows: $$\begin{aligned} D_0 = 4 dy - dx, \quad c_{EE} = 4 dy, \quad c_{NEE} = 4 dy - 2 dx \end{aligned}$$

void drawLine(int x0, int y0, int x1, int y1)
{
    int y = y0;
    const int dx = x1 - x0;
    const int dy = y1 - y0;
    const int c = dy + dy;
    const int c_ee = c + c;
    int d = c_ee - dx;
    const int c_nee = d - dx;
    const int end = x0 + ((dx >> 1) << 1);
    for (int x = x0; x < end; x += 2) {
        setPixel( x, y );
        if (d <= 0) {
            setPixel( x + 1, y );
            d += c_ee;
        }
        else {
            if (d <= c) setPixel( x + 1, y );
            else setPixel( x + 1, y + 1 );
            y++;
            d += c_nee;
        }
    }
    if (end != x1) setPixel( end, y );
}

Symmetry

Since lines are symmetric about the center, it is possible to make this algorithm more faster by plotting from both ends simultaneously. However, while the above algorithms draw lines in the exclusive range, the code below uses symmetry in the inclusive range. Besides, this algorithm may not exactly match the results from the above ones because of rounding. Although this algorithm considers only slopes between $0$ and $1/2$, this algorithm can be updated in a similar manner for any slopes outside this range.

void drawLineSymmetry(int x0, int y0, int x1, int y1)
{
    const int dx = x1 - x0;
    const int dy = y1 - y0;
    const int c = dy + dy;
    const int c_ee = c + c;
    int d = c_ee - dx;
    const int c_nee = d - dx;
    const int pairs = (dx + 1) >> 2;
    for (int i = 0; i < pairs; ++i) {
        setPixel( x0++, y0 );
        setPixel( x1--, y1 );
        if (d <= 0) {
            setPixel( x0++, y0 );
            setPixel( x1--, y1 );
            d += c_ee;
        }
        else {
            if (d <= c) {
                setPixel( x0++, y0++ );
                setPixel( x1--, y1-- );
            }
            else {
                setPixel( x0++, ++y0 );
                setPixel( x1--, --y1 );
            }
            d += c_nee;
        }
    }

    const int remaining = dx + 1 - (pairs << 2);
    if (remaining > 0) setPixel( x0++, y0 );
    if (remaining > 1) setPixel( x1, y1 );
    if (remaining > 2) {
        if (d <= c) setPixel( x0, y0 );
        else setPixel( x0, ++y0 );
    }
}

References

[1] 3D Graphics Programming Using OpenGL: Introduction

[2] Andrew S. Glassner (Ed.). 1990. Graphics gems. Academic Press Professional, Inc., USA.