Counting Bits

• 1. Counting 1-Bits
• 2. Comparing Two pop’s
• 3. Counting Leading 0’s
• 4. Counting Trailing 0’s
• Reference

1. Counting 1-Bits

Counting the number of 1-bits in a word is sometimes called population count, or pop(x). Although there may be a built-in function to do this, the algorithm itself is sometimes needed. Let $x = a_0 + a_1 2 + \cdots a_{31} 2^{31}$ for $a_i \in \{ 0, 1 \}$. Then, $a_i$ can be obtained as follows. $$\begin{aligned} \left \lfloor \frac{x}{2} \right \rfloor &= \left \lfloor \frac{a_0}{2} + a_1 + \cdots + a_{31} 2^{30} \right \rfloor = \left \lfloor \frac{a_0}{2} \right \rfloor + a_1 + \cdots + a_{31} 2^{30} \\ &= a_1 + \cdots + a_{31} 2^{30} \\\\ \left \lfloor \frac{x}{2^2} \right \rfloor &= \left \lfloor \frac{a_0}{2^2} + \frac{a_1}{2} + a_2 + \cdots + a_{31} 2^{29} \right \rfloor = \left \lfloor \frac{a_0}{2^2} + \frac{a_1}{2} \right \rfloor + a_2 + \cdots + a_{31} 2^{30} \\ &= a_2 + \cdots + a_{31} 2^{29} \\ &\; \vdots \\ \left \lfloor \frac{x}{2^i} \right \rfloor &= a_i + \cdots + a_{31} 2^{31 - i} \\\\ \left \lfloor \frac{x}{2^{i + 1}} \right \rfloor &= a_{i + 1} + \cdots + a_{31} 2^{30 - i} \\\\ \implies a_i &= \left \lfloor \frac{x}{2^i} \right \rfloor - 2 \left \lfloor \frac{x}{2^{i + 1}} \right \rfloor \end{aligned}$$

Note that $\left \lfloor x/2^{32} \right \rfloor = 0$ since $x < 2^{32}$. Therefore, the following interesting formula can be derived. $$\begin{aligned} \text{pop}(x) &= \sum_0^{31} a_i = \left \lfloor x \right \rfloor - 2 \left \lfloor \frac{x}{2} \right \rfloor + \left \lfloor \frac{x}{2} \right \rfloor - 2 \left \lfloor \frac{x}{2^2} \right \rfloor + \cdots + \left \lfloor \frac{x}{2^{31}} \right \rfloor - 2 \left \lfloor \frac{x}{2^{32}} \right \rfloor \\\\ &= x - \left \lfloor \frac{x}{2} \right \rfloor - \left \lfloor \frac{x}{2^2} \right \rfloor - \cdots - \left \lfloor \frac{x}{2^{31}} \right \rfloor \end{aligned}$$

In general, this formula can be extended to other bases. Let $\beta$ be the base. Then, the sum of digits is calculated as follows. $$\begin{aligned} \text{sum of digits}(x) = x - (\beta - 1) \left \lfloor \frac{x}{\beta} \right \rfloor - (\beta - 1) \left \lfloor \frac{x}{\beta^2} \right \rfloor - \cdots \end{aligned}$$

To implement pop(x), the divide and conquer technique can be used in $\log_2 32 = 5$ steps. For example, pop(x) is executed as below for the word 1011 1100 0110 0011 0111 1110 1111 1111, and this concept can be written with code as well.

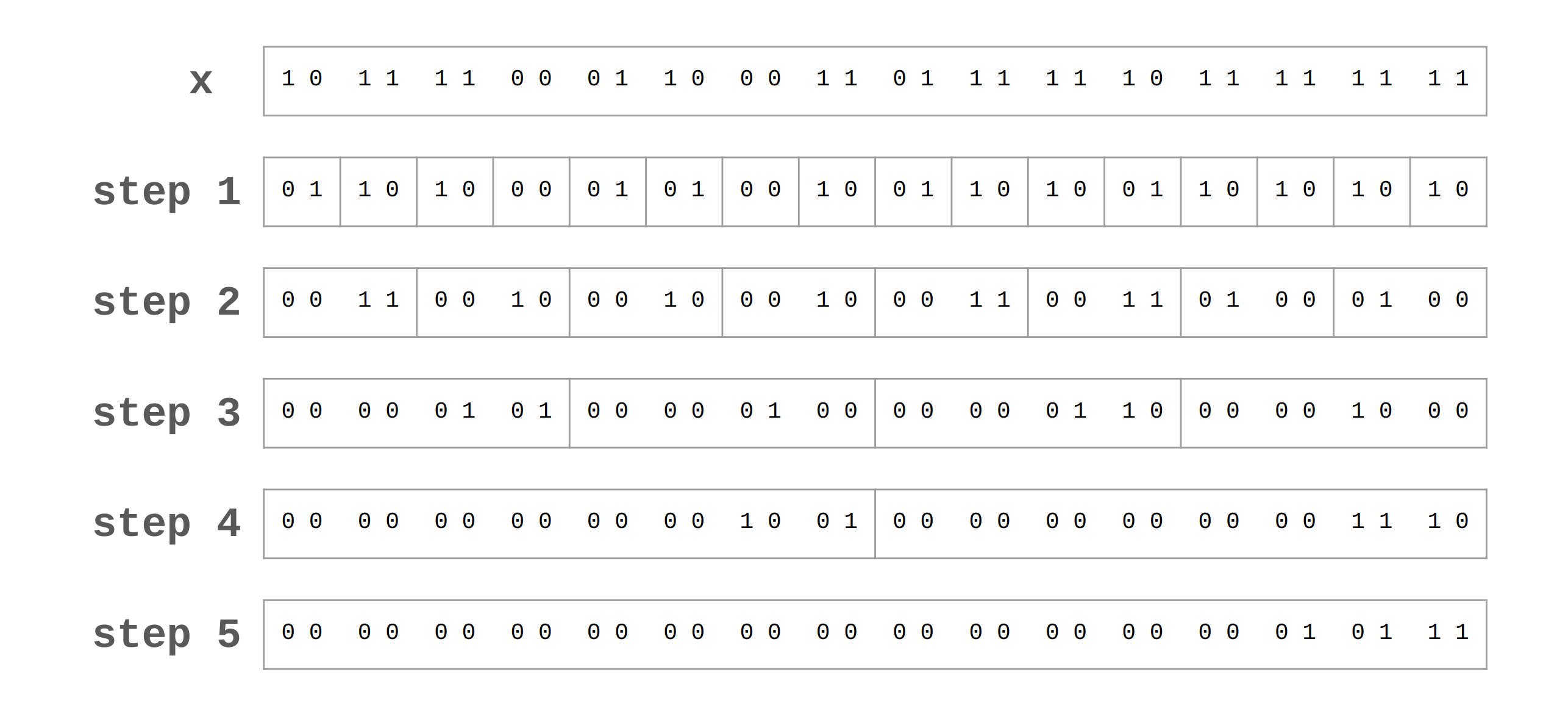
x = (x & 0x55555555) + ((x >> 1) & 0x55555555); // 0x55555555 == 0b10..10
x = (x & 0x33333333) + ((x >> 2) & 0x33333333); // 0x33333333 == 0b0011..0011
x = (x & 0x0f0f0f0f) + ((x >> 4) & 0x0f0f0f0f);  
x = (x & 0x00ff00ff) + ((x >> 8) & 0x00ff00ff);  
x = (x & 0x0000ffff) + ((x >> 16) & 0x0000ffff); 

Clearly, the last ((x >> 16) & 0x0000ffff) is unnecessary, and other &’s can be omitted when there is no danger that a field’s sum will carry over into the adjacent field. Furthermore, the formula of pop(x) derived previously makes the first line use one fewer instruction. As such, the more simplified code is as follows.

int pop(unsigned int x)
{
    x = x - ((x >> 1) & 0x55555555);
    x = (x & 0x33333333) + ((x >> 2) & 0x33333333);
    x = (x + (x >> 4)) & 0x0f0f0f0f;
    x = x + (x >> 8);
    x = x + (x >> 16);
    return x & 0x3f;
}

2. Comparing Two pop’s

There is a way to compare the population counts of two words without the actual counts. Of course, it is possible to compare them after calling pop() twice. However, the more clever idea is to clear a single bit in each word until one of the words is all zero. The other word then has the larger population count.

int comparePop(unsigned int x, unsigned int y)
{
    // pop(x) < pop(y) -> return a negative integer
    // pop(x) == pop(y) -> return 0
    // pop(x) > pop(y) -> return 1
    unsigned int a = x & ~y; // clear bits where both are 1 for x
    unsigned int b = y & ~x; // clear bits where both are 1 for y
    while (true) {
       if (a == 0) return b | -b;
       if (b == 0) return 1;
       a = a & (a - 1); // turn off the rightmost 1-bit
       b = b & (b - 1); // turn off the rightmost 1-bit
    }
}

After clearing the common 1-bits in each 32-bit word, the maximum possible number of 1-bits in both words together is 32. So, the loop is run a maximum of 16 times. Note that b | -b and a & (a - 1) are techniques discussed previously. Particularly, since ~(b | -b) turns off all bits but turns on the trailing 0’s only, b | -b can be considered inversely.

3. Counting Leading 0’s

Although there may be a built-in function to count leading 0’s, a simple way to implement this is using a binary search technique.

int clz(unsigned int x)
{
    if (x == 0) return 32;
    
    int n = 1;
    if ((x >> 16) == 0) { n += 16; x = x << 16; }
    if ((x >> 24) == 0) { n += 8; x = x << 8; }
    if ((x >> 28) == 0) { n += 4; x = x << 4; }
    if ((x >> 30) == 0) { n += 2; x = x << 2; }
    return n - (x >> 31);
}

However, there is a much better way to implement clz() using pop(). The following five assignments to x can be done in any order. The idea is to remove all the non-leading 0’s, and then count the number of 0’s with pop(~x).

int clz(unsigned int x)
{   
    x = x | (x >> 1);
    x = x | (x >> 2);
    x = x | (x >> 4);
    x = x | (x >> 8);
    x = x | (x >> 16);
    return pop( ~x );
}

A novel application related to clz() is to generate exponentially distributed random integers by generating uniformly distributed random integers and taking clz() of the result. The result is 0 with probability 1/2, 1 with probability 1/4, 2 with probability 1/8, and so on.

4. Counting Trailing 0’s

In this case, the best way is using pop() or clz(). That is, 32 - clz(~x & (x - 1)), pop(~x & (x - 1)), or 32 - pop(x | -x) works when referencing techniques discussed previously. However, this algorithm can be also implemented with a binary search technique as follows.

int ctz(unsigned int x)
{
    if (x == 0) return 32;
    
    int n = 1;
    if ((x & 0x0000ffff) == 0) { n += 16; x = x >> 16; }
    if ((x & 0x000000ff) == 0) { n += 8; x = x >> 8; }
    if ((x & 0x0000000f) == 0) { n += 4; x = x >> 4; }
    if ((x & 0x00000003) == 0) { n += 2; x = x >> 2; }
    return n - (x & 1);
}

It is interesting that if the number $x$ is uniformly distributed, then the average number of trailing 0’s is almost 1. Let $p_i$ be the probability that there are exactly $i$ trailing 0’s. Then, the average number $M$ is $$\begin{aligned} M &= \sum_i i p_i = 0 \cdot \frac{1}{2} + 1 \cdot \frac{1}{2^2} + 2 \cdot \frac{1}{2^3} + 3 \cdot \frac{1}{2^4} + \cdots = \sum_i \frac{i}{2^{i + 1}} \\\\ \implies M &= 2M - M = \sum_i \frac{i}{2^i} - \frac{i}{2^{i + 1}} \\\\ &= \frac{1}{2} + \left( \frac{2}{2^2} - \frac{1}{2^2} \right) + \left( \frac{3}{2^3} - \frac{2}{2^3} \right) + \cdots = \frac{1}{2} + \frac{1}{2^2} + \frac{1}{2^3} + \cdots \\\\ &= \cfrac{\cfrac{1}{2}}{1 - \cfrac{1}{2}} = 1 \end{aligned}$$

Especially, $M \approx 0.999999996041$ for a 32-bit word.

Reference

[1] Henry S. Warren. 2012. Hacker’s Delight (2nd. ed.). Addison-Wesley Professional.