Repeated Combination

• Definition
• Derivation
• Another Point of View

Definition

A $r$-combination with repetitions, or $r$-multicombination from a set $S$ of size $n$ is defined by $$\begin{aligned} \left( \!\! \binom{n}{r} \!\! \right) = \binom{n + r - 1}{r} \end{aligned}$$

Since it is a combination, the arrangement of the members in $S$ does not matter. However, the difference is that it is a sample of $r$ elements from a set of $n$ elements allowing for duplicates.

Derivation

First, consider $S = \{ 1, 2, 3 \}$. All possible cases of the repeated combination are as follows. $$\begin{equation} \{ 1, 1 \}, \{ 1, 2 \}, \{ 1, 3 \}, \{ 2, 2 \}, \{ 2, 3 \}, \{ 3, 3 \} \end{equation}$$

If $0$ and $1$ are added to the first and second elements of each of them, $$\begin{equation} \{ 1, 2 \}, \{ 1, 3 \}, \{ 1, 4 \}, \{ 2, 3 \}, \{ 2, 4 \}, \{ 3, 4 \} \end{equation}$$

It is a combination of $n$ things taken $r$ at a time without repetition. Furthermore, since the case (1) and (2) are one-to-one correspondence, $\left( \!\! \dbinom{3}{2} \!\! \right) = \dbinom{4}{2} = 6$. Generally speaking, $\left( \!\! \dbinom{n}{r} \!\! \right)$ can be analyized as follows. $$\begin{aligned} \begin{array}{ccc} \left( \!\! \dbinom{n}{r} \!\! \right) & & \dbinom{n + r - 1}{r} \\\\ \hline \\ \{ 1, 1, 1, \cdots, 1 \} & & \{ 1, 2, 3, \cdots, r \} \\\\ \{ 1, 1, 1, \cdots, 2 \} & & \{ 1, 2, 3, \cdots, r + 1 \} \\ \vdots & \implies \text{ adding } \{ 0, 1, \cdots, r - 1 \} \implies & \vdots \\ \{ 2, 2, 2, \cdots, 2 \} & & \{ 2, 3, 4, \cdots, r + 1 \} \\ \vdots & & \vdots \\ \{ n, n, n, \cdots, n \} & & \{ n, n + 1, n + 2, \cdots, n + r - 1 \} \end{array} \end{aligned}$$

Therefore, the repeated combination selecting $r$ elements from distinct $n$ elements is equal to the combination selecting $r$ elements from distinct $(n + r - 1)$ elements.

Another Point of View

Consider the number of cases selecting 2 among 3 characters, $a$, $b$, and $c$ allowing duplicates. This can be thought of as when putting 2 balls of the same color into 3 baskets, the characters correspond to the number of balls in each basket.

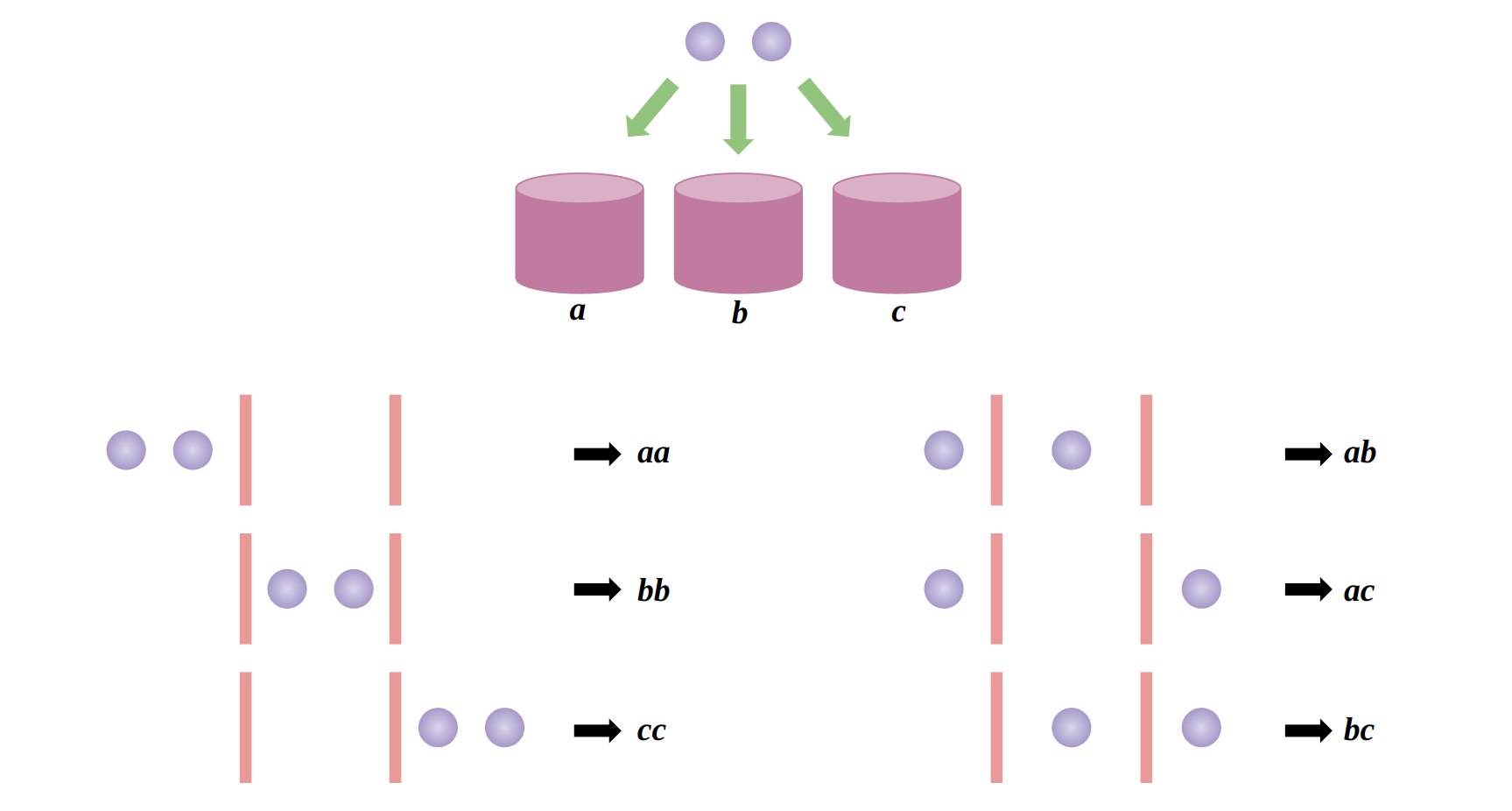
As shown above, this is also the same as the number of cases arranging 2 balls and 2 separating bars. Generally speaking, $\left( \!\! \dbinom{n}{r} \!\! \right)$ is the number of cases arranging $r$ balls and $(n - 1)$ separating bars. $$\begin{aligned} \left( \!\! \binom{n}{r} \!\! \right) = \frac{(n + r - 1)!}{(n - 1)! r!} = \binom{n + r - 1}{r} \end{aligned}$$