023. Circle in Circle

For a circle $O$ with diameter $\overline{AB}$, there exists a chord $l$ perpendicular to $\overline{AB}$. Suppose there exists a circle $O_1$ inside circle $O$ such that $O_1$ is tangent to circle $O$ at point $P$ and tangent to $l$ at point $Q$. Prove that the line $\overline{PQ}$ intersects $\overline{AB}$ on circle $O$.

---

Consider the situation shown in the figure below.

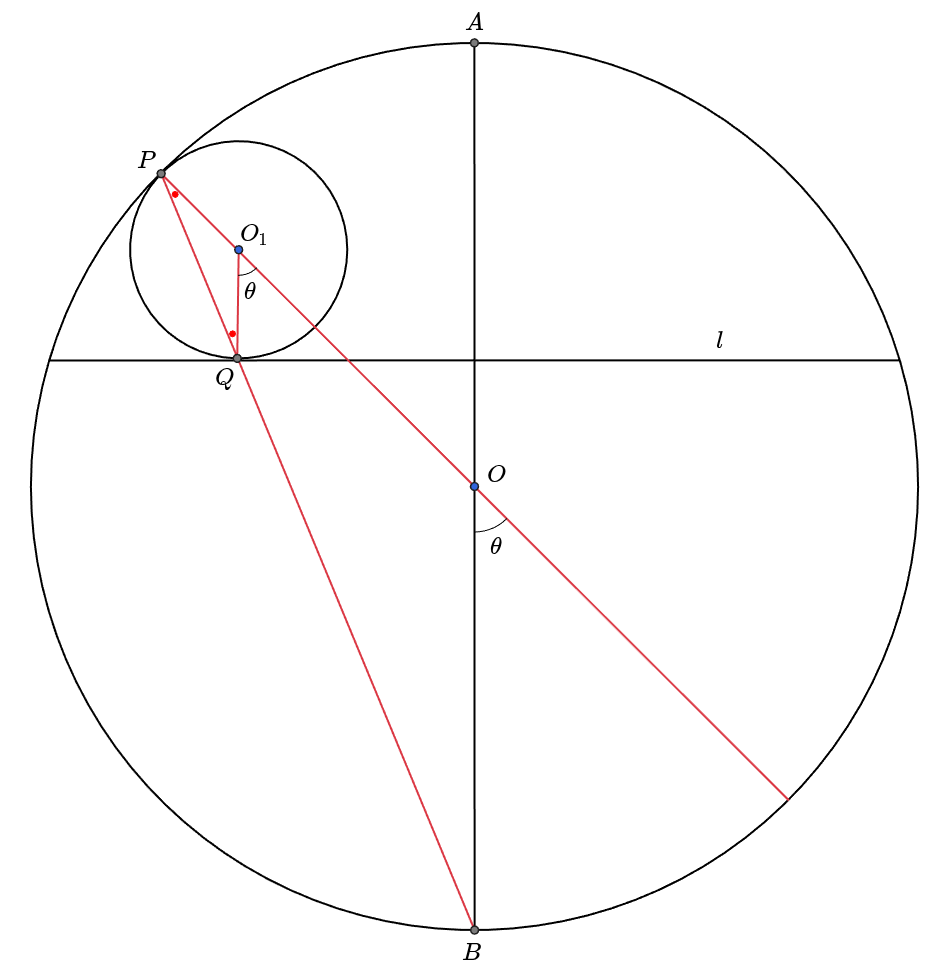
The tangent line at point $P$ on circle $O$ is perpendicular to both $\overline{PO_1}$ and $\overline{PO}$, so points $P$, $O_1$, and $O$ lie on the same line.

Let $\theta$ denote the smaller angle formed by line $\overline{PO}$ and line $\overline{AB}$. Since $l$ is perpendicular to both $\overline{AB}$ and $\overline{QO_1}$, $\overline{AB}$ and $\overline{QO_1}$ are parallel. Therefore, $\angle{QO_1O} = \theta$.

Triangle $O_1PQ$ is isosceles, so $\angle{QPO_1} = \theta / 2$.

Therefore, by the property of inscribed angles, points $P$, $Q$, and $B$ lie on a straight line.