022. Maximum Angle

In right triangle $ABC$ with $\overline{AB} = 2$, $\overline{BC} = 100$, and $\angle{B} = 90°$, there is a point $P$ moving along $\overline{BC}$. Let $\theta$ be the maximum value of $\angle{APD}$ with respect to the midpoint $D$ of $\overline{AB}$. Find the value of $\sin \theta$.

---

The key is to draw the auxiliary circle. Let $O$ be the center of the circle passing through points $A$ and $D$ and tangent to $\overline{BC}$.

Let $E$ be the midpoint of $\overline{AD}$, and let $P$ lie one the point where the circle $O$ is tangent to $\overline{BC}$. The foot of the perpendicular line dropped from the center of the circle onto the chord bisects the chord, so $\angle{OEB} = 90°$. Since $\angle{EBP} = \angle{OPB} = 90°$, $\Box{OEBP}$ is a rectangle. Therefore, the radius of circle $O$ is $\overline{OP} = 1 + 1/2 = 3/2$, so $\overline{OA} = 3/2$.

Then, $\angle{APD} = \angle{AOE} = \theta$ is the maximum value. As shown in the figure below, suppose point $P$ does not lie on circle $O$. Let $Q$ be the point where a line passing through $P$ and perpendicular to $\overline{BC}$ intersects circle $O$. Then, since point $P$ lies outside circle $O$, $\angle{APD} < \angle{AQD} = \theta$.

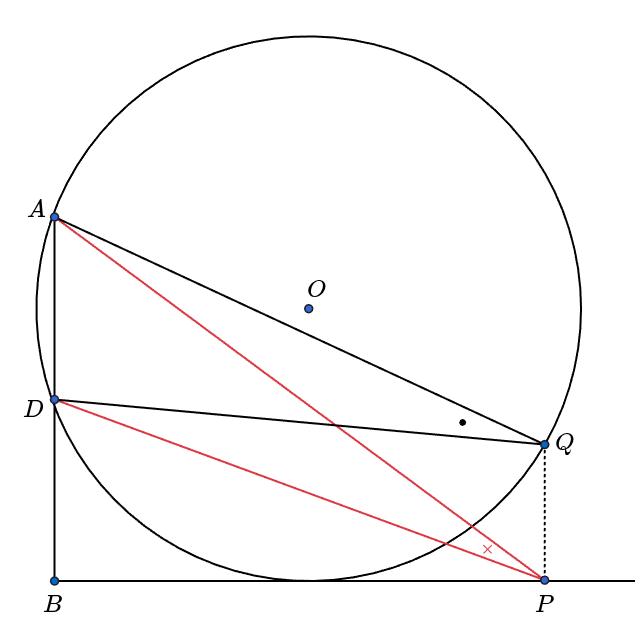
That is, when point $P$ lies on circle $O$, $\angle{APD}$ is maximized. Therefore, $\sin \theta = \overline{AE} / \overline{OA} = (1/2) / (3/2) = 1/3$.