019. Tiling

Prove that the following two propositions are equivalent when $m$ and $n$ are natural numbers greater than or equal to 2.

• $mn$ is a multiple of 8.
• Using multiple shapes in the following figure, a rectangle with width $m$ and height $n$ can be tiled.

---

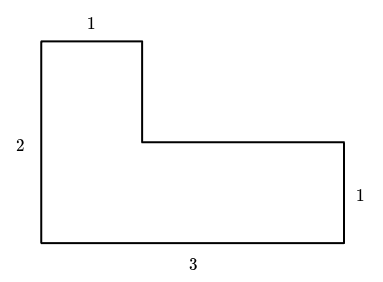
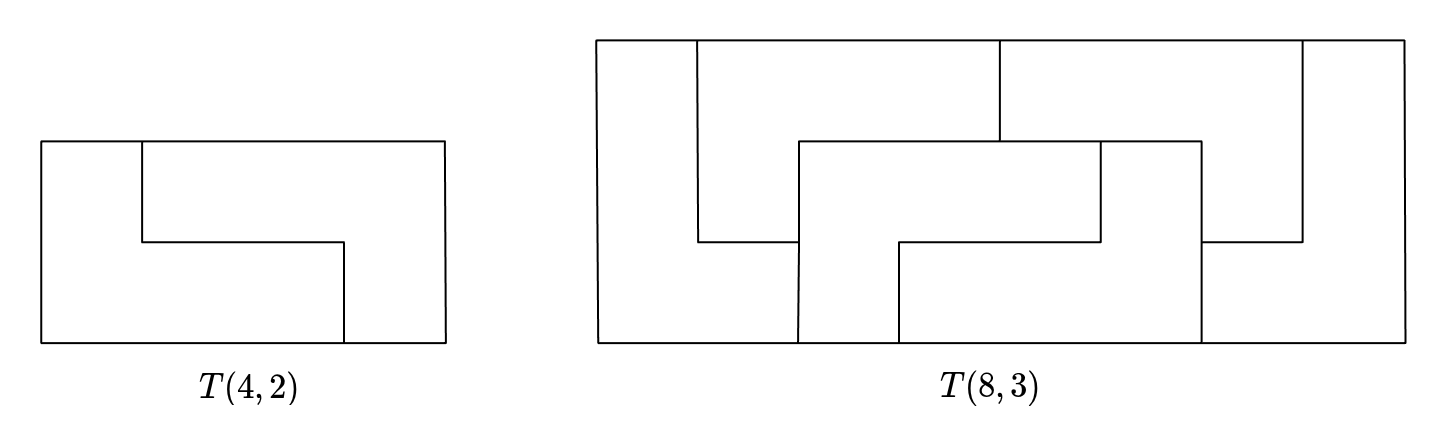
Let $T(m, n)$ be the tiled rectangle with width $m$ and height $n$ using the above shape. Then, $T(4, 2)$ and $T(8, 3)$ are possible as follows.

Since $T(m, n) = T(n, m)$, the condition that $mn$ is a multiple of 8 can be considered only in the following two cases.

• case 1: $m$ is a multiple of 4 and $n$ is even.
  • $T(m, n)$ is possible because it is a combination of multiple $T(4, 2)$.
• case 2: $m$ is a multiple of 8 and $n$ is odd.
  • $T(m, n)$ can be tiled by dividing it into $T(m, 3)$ and $T(m, n - 3)$. Here, $T(m, 3)$ can be made by combining multiple $T(8, 3)$, and $T(m, n - 3)$ is also possible because it corresponds to case 1.

Now, to prove the converse, assume that there exists some possible tiling $T(m, n)$. Since the area of ​​this L-shaped figure is 4, $mn$ is a multiple of 4. That is, since at least one of $m$ and $n$ is even, let $m$ be even.

Let’s divide $T(m, n)$ into unit squares and assign 1, -1, 0 to each unit square as follows.

• Odd rows: 1, -1, 1, -1, $\cdots$, 1, -1
  • Since $m$ is even, the total number assigned is even.
• Even rows: all 0s

Then, no matter how the L-shaped figure is placed inside $T(m, n)$, the sum of the numbers inside this shape is either 1 or -1. As can be seen in the figure below, the result is the same even when symmetrically placed.

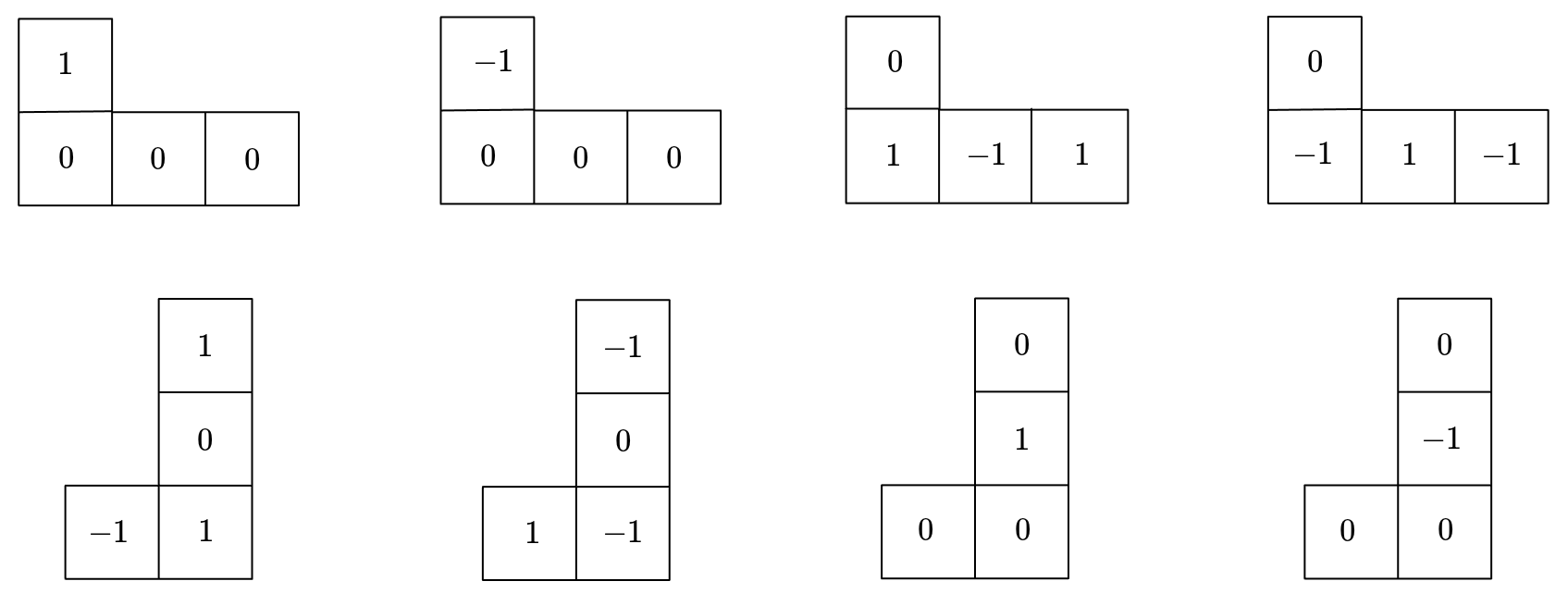
However, since the sum of all numbers inside $T(m, n)$ is 0, the number of the L-shaped figures whose inner sum is 1 and the number of the ones whose inner sum is -1 are equal. That is, the number of the L-shaped figures that make up $T(m, n)$ is even. Therefore, the area of $​​T(m, n)$ is $4 * 2k$, so $mn$ is a multiple of 8.