015. Incidence of Rays to the Corner

Point $P$ on a square $ABCD$ with one side length of $1$ moves in a straight line from point $A(0, 1)$ to point $(a, 0)$ where $0 < a < 1$. When point $P$ reaches one of the sides and continues its motion by reflecting, find all values ​​of $a$ that allow point $P$ to reach any of the four corners $A$, $B$, $C$, and $D$.

---

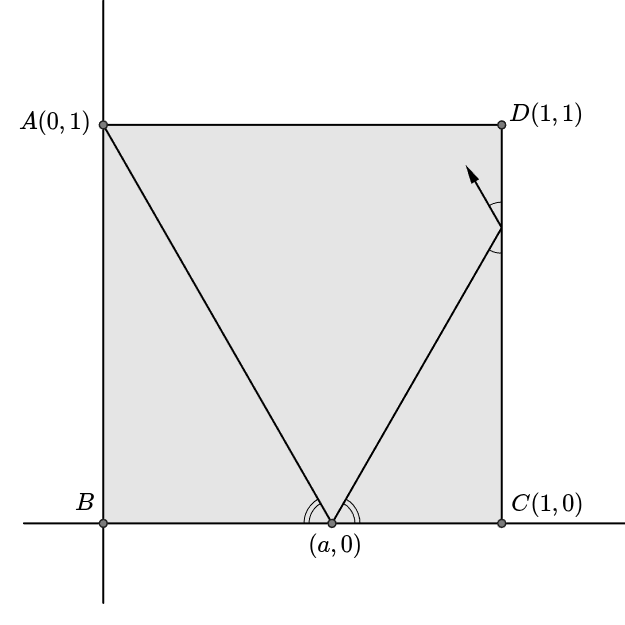
If the path is expanded symmetrically with respect to the sides of the square $ABCD$ as follows, $E''$ expands to $E$, $F''$ expands to $F'$, and $F'$ expands to $F$, ultimately forming a straight line $\overrightarrow{AP}$. When this path reaches a corner of a square, $\overrightarrow{AP}$ also passes through the grid point.

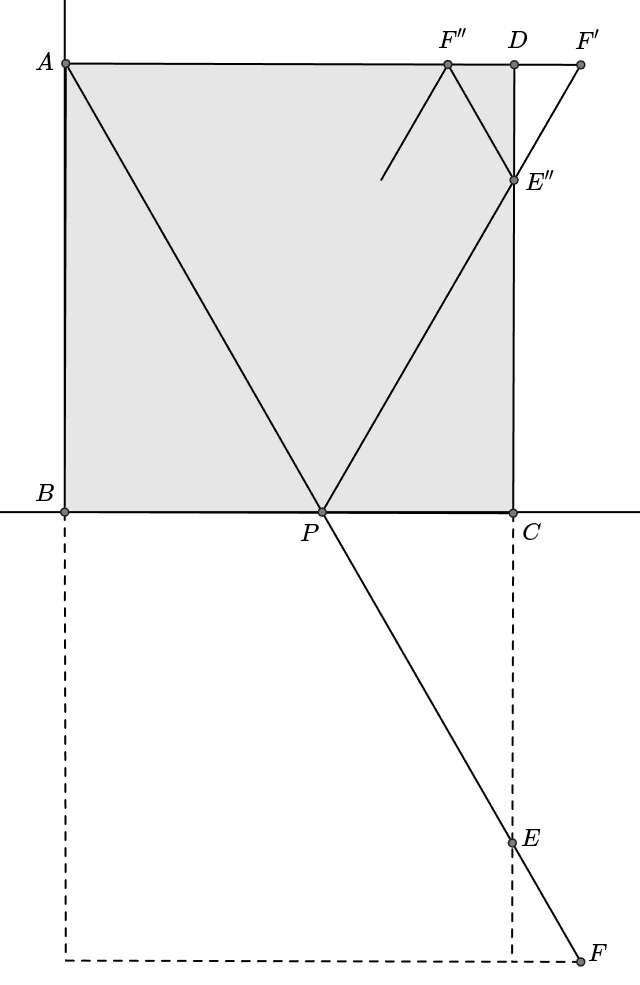
Let this grid point be $(m, -n)$ where $m$ and $n$ are natural numbers. Then, the line equation of $\overrightarrow{AP}$ is $y = -(n + 1)x / m + 1$. Therefore, when $y = 0$, $x = m / (n+1) = a$, which implies $a$ is a rational number.

Meanwhile, for any rational number $a$ such that $0 < a < 1$, there exist natural numbers $m$ and $n$ that satisfy $a = m / (n+1)$. This is because if $a = m/n'$ where $n'$ is a natural number, then $m < n'$ since $0 < a < 1$, as such $1 \leq m < n'$. That is, $n'$ is a natural number greater than or equal to $2$, and can be replaced with $n + 1$. Here, $\overrightarrow{AP}$ passes through $(m, -n)$, so $a$ to be found is all positive rational numbers less than $1$.