007. Types of the Triangle

Let $M$ be the midpoint of $\overline{BC}$ of a triangle $ABC$. Determine the types of this triangle if $\angle BAM + \angle ACB = 90\degree$.

---

First, note that $\angle C$ cannot be an obtuse angle or right angle to satisfy the condition. Besides, $\angle B$ cannot be an obtuse angle or right angle as well because $\angle BAM \ne \angle CAH$ where $H$ is the perpendicular from $A$ to the line $BC$.

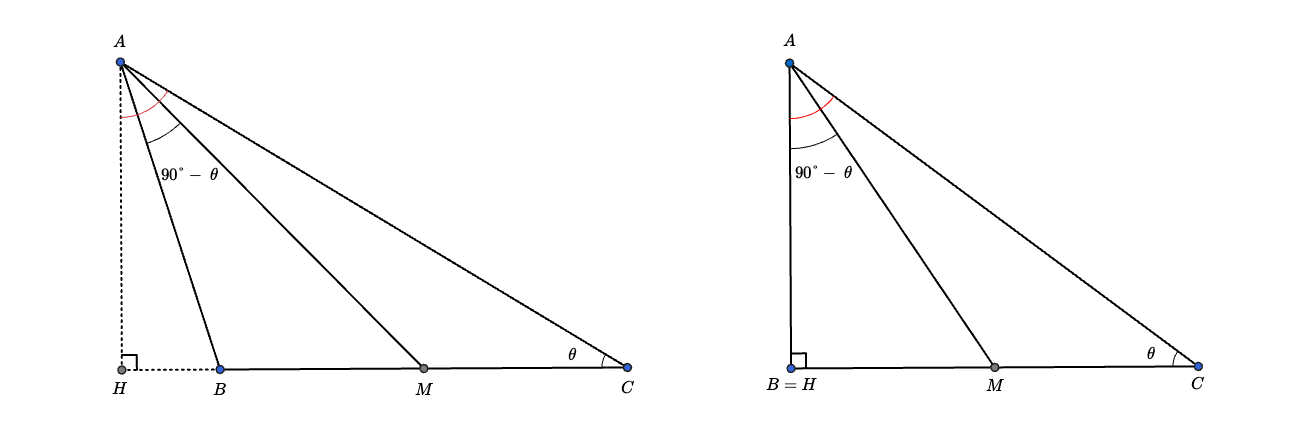
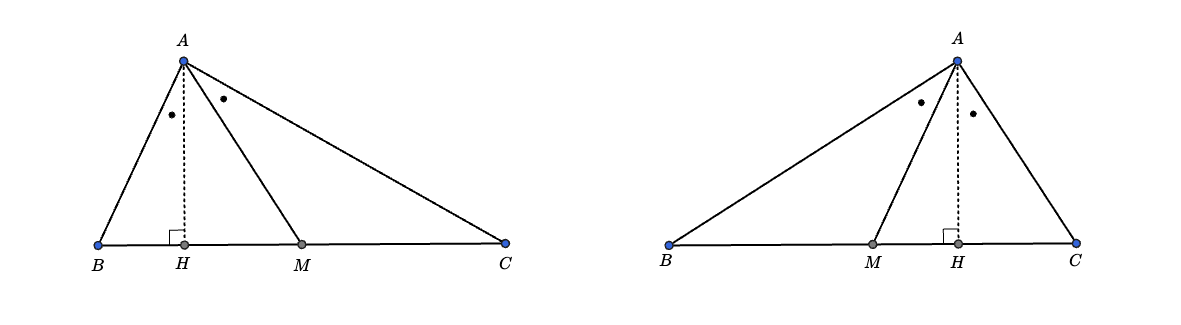
Therefore, $H$ must be on $\overline{BC}$ except for $B$ and $C$. The following two triangles satisfy $\angle BAM = \angle CAH$ and can become candidates.

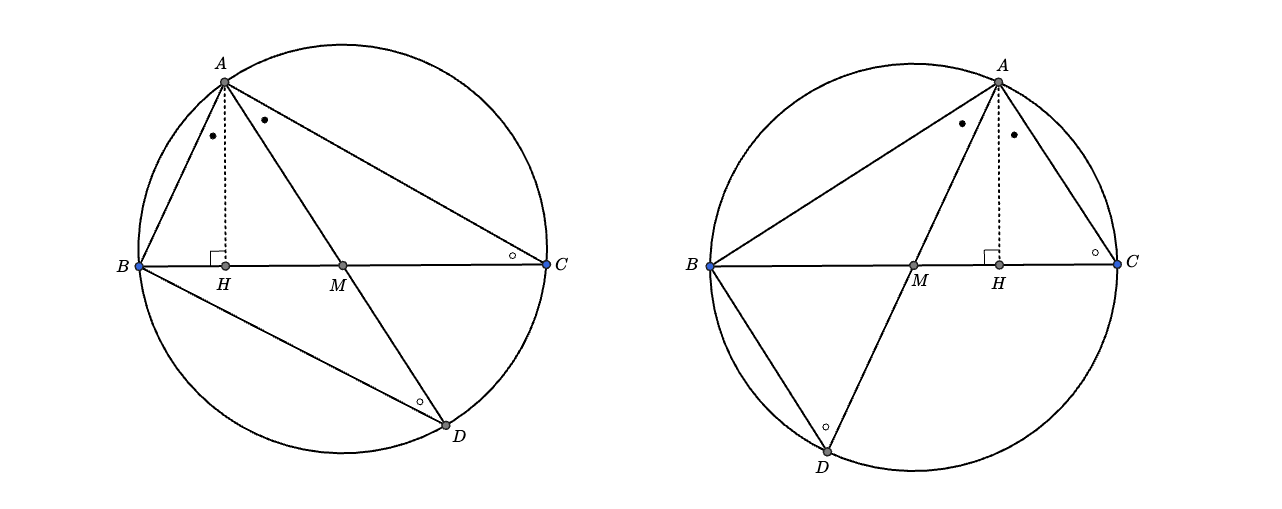
Now, let $D$ be the intersection between the circumcircle of $ABC$ and the line $AM$, which is not $A$. Then, by inscribed angle theorem, $\angle ACB = \angle ADB$ and $\angle ABD = 90 \degree$. That is, $\overline{AD}$ is a diameter of this circumcircle.

Accordingly, since $\overline{AD}$ passes through the midpoint $M$, $\overline{BC}$ is a diameter or $\overline{BC} \perp \overline{AD}$.

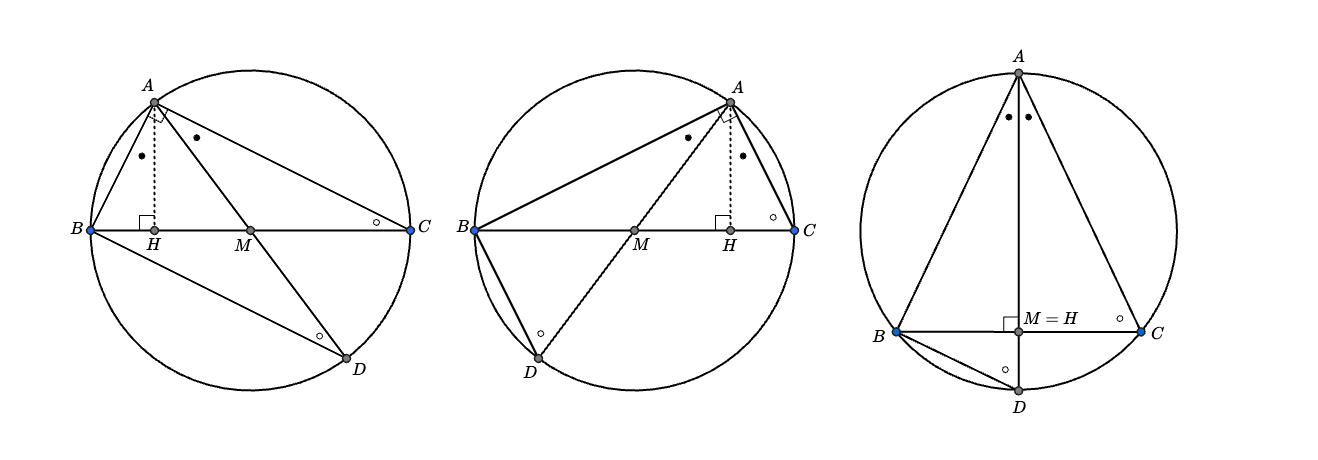
Therefore, the triangle $ABC$ are a right triangle with its right angle at $A$ or an isosceles triangle such that $\overline{AB} = \overline{AC}$.