005. Ticket Office with No Small Change

13 students are waiting in line to buy tickets to a museum where the admission fee is 50 cents. 5 of them each have a one-dollar bill, and the other 8 each have a 50-cent coin. At first, there was no change at the ticket office, so change could not be received, and each person should only buy one ticket. Find out how many ways to wait in line so that no student has to wait because they cannot get change. It is considered the same case if students with the same money change their order in a line.

---

Let $a$ and $b$ be a student with a 50-cent coin and a student with a one-dollar bill. Then, 13 students in line can be viewed as a sequence consisting of 8 $a$’s and 5 $b$’s. In order to receive change right away, the number of $a$’s must be greater than or equal to the number of $b$’s, no matter which student is selected starting from the first student. So, this is the exactly same with the number of cases going $A$ to $B$ as below when $a$ corresponds to the right-move and $b$ corresponds to the up-move.

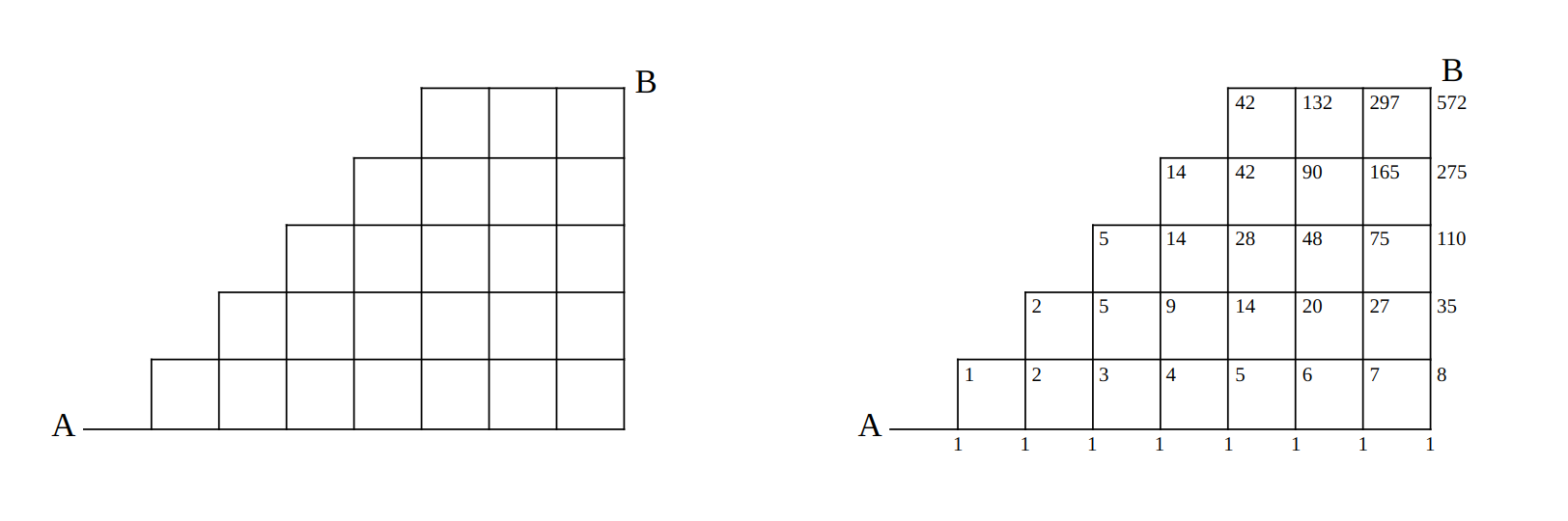
Therefore, the number of cases is 572.