001. The Number of Vertices

Find the number of vertices of a convex polyhedron composed of only regular pentagons and regular hexagons where five regular hexagons are linked per one regular pentagon.

---

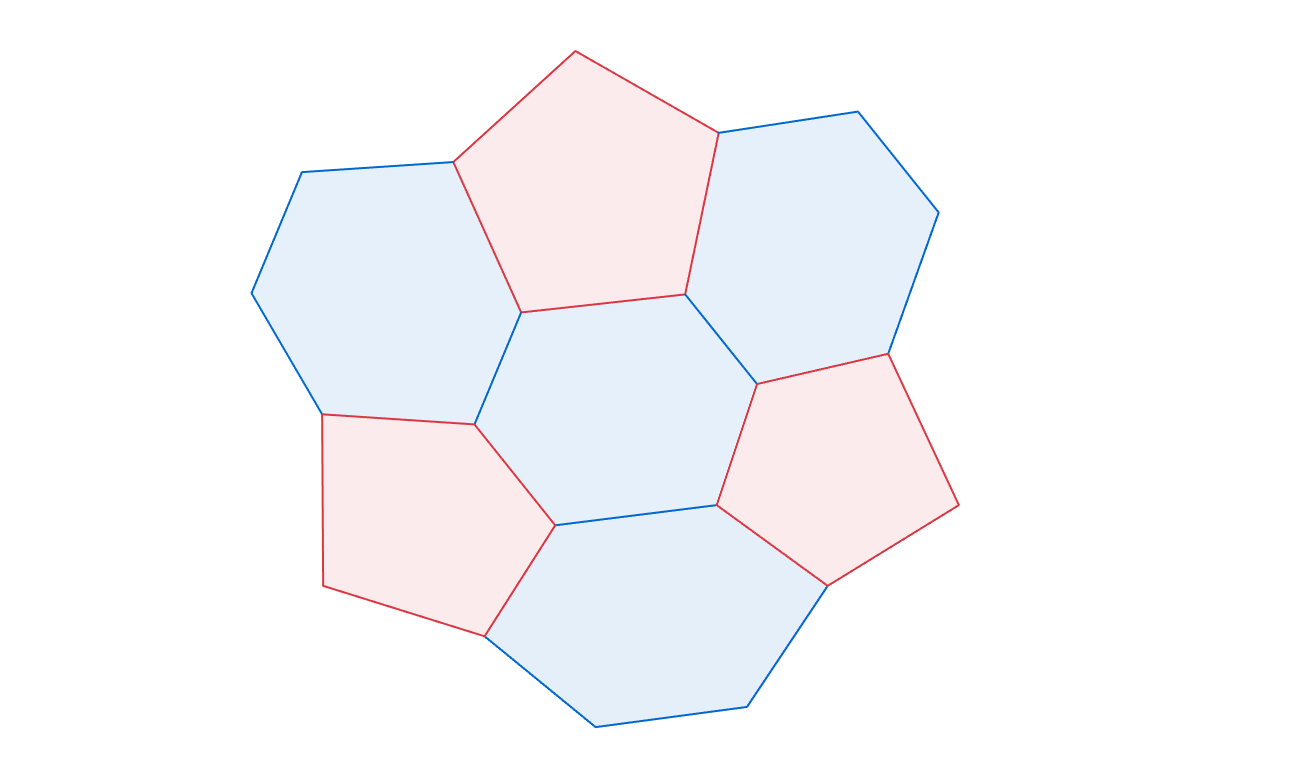
Let $v$, $e$, and $f$ be the number of vertices, edges, and faces of this polyhedron. Also, $a$ is the number of regular pentagons and $b$ is the number of regular hexagons. Then, 5 regular hexagons are linked per one regular pentagon and 3 pentagons per one regular hexagon. Note that it is not that 6 pentagons per one regular hexagon. So, $$\begin{aligned} 5a = 3b \end{aligned}$$

Besides, 3 edges per one vertex and 2 vertices per one edge. $$\begin{aligned} 3v = 2e \end{aligned}$$

Since 5 edges per one regular pentagon face and 6 edges per one regular hexagon face, the total number of edges is $$\begin{aligned} e = \frac{5a + 6b}{2} \end{aligned}$$

Note that all edges are counted twice so the division must be considered. $$\begin{aligned} \frac{3v}{2} = \frac{5a + 6b}{2} \implies v = \frac{5a + 6b}{3} \end{aligned}$$

By Euler characteristic, $v - e + f = 2$, $$\begin{aligned} \frac{5a + 6b}{3} - \frac{5a + 6b}{2} + (a + b) = 2 \end{aligned}$$

Combining with $5a = 3b$, $a = 12$ and $b = 20$. Therefore, $v = 60$.

In fact, the number of vertices of this polyhedron is $v = 5a$ because it is the same as the total number of vertices of all regular pentagons.